Previous Page
   Next Page
 
Evokation
  
 
Index
  

 

A

MAZE

IN

ZAZAZA ENTER ZAZAZA

ZAZAZAZAZAZAZAAZAZAZAZAZAZAZ

ZAZAZAZAZAZAZAZAZAAZAZAZAZAZAZAZAZAZ

THE

MAGICALALPHABET

ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA

 12345678910111213141516171819202122232425262625242322212019181716151413121110987654321

 

 

WORK DAYS OF GOD

Herbert W Morris D.D.circa 1883

Page 22

"As all the words in the English language are composed out of the twenty-six letters of the alphabet,.."

 

 

LIGHT AND LIFE

Lars Olof Bjorn 1976

Page 197

"By writing the 26 letters of the alphabet in a certain order one may put down almost any message (this book 'is written with the same letters' as the Encyclopaedia Britannica and Winnie the Pooh, only the order of the letters differs). In the same way Nature is able to convey with her language how a cell and a whole organism is to be constructed and how it is to function. Nature has succeeded better than we humans; for the genetic code there is only one universal language which is the same in a man, a bean plant and a bacterium."

"BY WRITING THE 26 LETTERS OF THE ALPHABET IN A CERTAIN ORDER

ONE MAY PUT DOWN ALMOST ANY MESSAGE"

 

 

A
B
C
D
E
F
G
H
I
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
J
K
L
M
N
O
P
Q
R
10
11
12
13
14
15
16
17
18
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
S
T
U
V
W
X
Y
Z
I
19
20
21
22
23
24
25
26
9
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
ME
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
I
ME
I
ME
I
ME
I
ME
I
9
18
9
18
9
18
9
18
9
=
1+8
=
1+8
=
1+8
=
1+8
=
=
9
=
9
=
9
=
9
=
I
ME
I
ME
I
ME
I
ME
1
9
9
9
9
9
9
9
9
9
I
ME
I
ME
I
ME
I
ME
1

 

 

A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

 

 

"BY WRITING THE 26 LETTERS OF THE ALPHABET IN A CERTAIN ORDER

ONE MAY PUT DOWN ALMOST ANY MESSAGE"

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
=
7
=
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
=
7
=
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
=
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
=
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
=
9
=
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
=
9
=
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
=
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
=
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
=
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

A

HISTORY OF GOD

Karen Armstrong

The God of the Mystics

Page 250

"(The Book of Creation). There is no attempt to describe the creative process realistically; the account is unashamedly symbolic and shows God creating the world by means of language as though he were writing a book. But language has been entirely transformed and the message of creation is no longer clear. Each letter of the Hebrew alphabet is given a numerical value; by combining the letters with the sacred numbers, rearranging them in endless configurations, the mystic weaned his mind away from the normal connotations of words."  

 

 

A
B
C
D
E
F
G
H
I
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
J
K
L
M
N
O
P
Q
R
10
11
12
13
14
15
16
17
18
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
S
T
U
V
W
X
Y
Z
I
19
20
21
22
23
24
25
26
9
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
ME
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
I
ME
I
ME
I
ME
I
ME
I
9
18
9
18
9
18
9
18
9
=
1+8
=
1+8
=
1+8
=
1+8
=
=
9
=
9
=
9
=
9
=
I
ME
I
ME
I
ME
I
ME
1
9
9
9
9
9
9
9
9
9
I
ME
I
ME
I
ME
I
ME
1

 

 

A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

FINGERPRINTS OF THE GODS

A QUEST FOR THE BEGINNING AND THE END

Graham Hancock 1995

Chapter 32

Speaking to the Unborn

Page 285

"It is understandable that a huge range of myths from all over the ancient world should describe geological catastrophes in graphic detail. Mankind survived the horror of the last Ice Age, and the most plausible source for our enduring traditions of flooding and freezing, massive volcanism and devastating earthquakes is in the tumultuous upheavals unleashed during the great meltdown of 15,000 to 8000 BC. The final retreat of the ice sheets, and the consequent 300-400 foot rise in global sea levels, took place only a few thousand years before the beginning of the historical period. It is therefore not surprising that all our early civilizations should have retained vivid memories of the vast cataclysms that had terrified their forefathers.
Much harder to explain is the peculiar but distinctive way the myths of cataclysm seem to bear the intelligent imprint of a guiding hand.l Indeed the degree of convergence between such ancient stories is frequently remarkable enough to raise the suspicion that they must all have been 'written' by the same 'author'.
Could that author have had anything to do with the wondrous deity, or superhuman, spoken of in so many of the myths we have reviewed, who appears immediately after the world has been shattered by a horrifying geological catastrophe and brings comfort and the gifts of civilization to the shocked and demoralized survivors?
White and bearded, Osiris is the Egyptian manifestation of this / Page 286 / universal figure, and it may not be an accident that one of the first acts he is remembered for in myth is the abolition of cannibalism among the primitive inhabitants of the Nile Valley.2 Viracocha, in South America, was said to have begun his civilizing mission immediately after a great flood; Quetzalcoatl, the discoverer of maize, brought the benefits of crops, mathematics, astronomy and a refined culture to Mexico after the Fourth Sun had been overwhelmed by a destroying deluge.
Could these strange myths contain a record of encounters between scattered palaeolithic tribes which survived the last Ice Age and an as yet unidentified high civilization which passed through the same epoch?
And could the myths be attempts to communicate?

A message in the bottle of time"

'Of all the other stupendous inventions,' Galileo once remarked,

what sublimity of mind must have been his who conceived how to communicate his most secret thoughts to any other person, though very distant either in time or place, speaking with those who are in the Indies, speaking to those who are not yet born, nor shall be this thousand or ten thousand years? And with no greater difficulty than the various arrangements of two dozen little signs on paper? Let this be the seal of all the admirable inventions of men.3

If the 'precessional message' identified by scholars like Santillana, von Dechend and Jane Sellers is indeed a deliberate attempt at communication by some lost civilization of antiquity, how come it wasn't just written down and left for us to find? Wouldn't that have been easier than encoding it in myths? Perhaps.
Nevertheless, suppose that whatever the message was written on got destroyed or worn away after many thousands of years? Or suppose that the language in which it was inscribed was later forgotten utterly (like the enigmatic Indus Valley script, which has been studied closely for more than half a century but has so far resisted all attempts at decoding)? It must be obvious that in such circumstances a written / Page 287 / legacy to the future would be of no value at all, because nobody would be able to make sense of it.
What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them - and the city of Teotihuacan may be the calling-card of a lost civilization written in the eternal language of mathematics.
Geodetic data, related to the exact positioning of fixed geographical points and to the shape and size of the earth, would also remain valid and recognizable for tens of thousands of years, and might be most conveniently expressed by means of cartography (or in the construction of giant geodetic monuments like the Great Pyramid of Egypt, as we shall see).
Another 'constant' in our solar system is the language of time: the great but regular intervals of time calibrated by the inch-worm creep of precessional motion. Now, or ten thousand years in the future, a message that prints out numbers like 72 or 2160 or 4320 or 25,920 should be instantly intelligible to any civilization that has evolved a modest talent for mathematics and the ability to detect and measure the almost imperceptible reverse wobble that the sun appears to make along the ecliptic against the background of the fixed stars..."

"What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them"

"WRITTEN IN THE ETERNAL LANGUAGE OF MATHEMATICS"

 

 

 

 

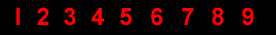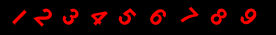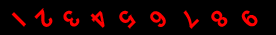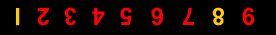
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

 

A
B
C
D
E
F
G
H
I
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
J
K
L
M
N
O
P
Q
R
10
11
12
13
14
15
16
17
18
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
S
T
U
V
W
X
Y
Z
I
19
20
21
22
23
24
25
26
9
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
ME
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
I
ME
I
ME
I
ME
I
ME
I
9
18
9
18
9
18
9
18
9
=
1+8
=
1+8
=
1+8
=
1+8
=
=
9
=
9
=
9
=
9
=
I
ME
I
ME
I
ME
I
ME
1
9
9
9
9
9
9
9
9
9
I
ME
I
ME
I
ME
I
ME
1

 

 

 

7
H
I
N
O
S
X
Z
-
-
-
-
-
--
-
8
9
14
15
19
24
26
+
=
115
1+1+5
=
7
7
H
I
N
O
S
X
Z
-
-
-
-
-
--
-
8
9
5
6
1
6
8
+
=
43
4+3
=
7
7
H
I
N
O
S
X
Z
-
-
-
-
-
-
H
Z
-
8
-
-
-
-
-
8
+
=
16
1+6
=
7
-
-
I
-
-
-
X
-
-
-
-
-
-
-
-
-
9
-
-
-
6
-
+
=
15
1+5
=
6
-
-
-
N
-
S
-
-
-
-
-
-
-
-
-
-
-
5
-
1
-
-
+
=
6
-
-
6
-
-
-
-
O
-
-
-
-
-
-
-
-
-
-
-
-
-
6
-
-
-
+
=
6
-
-
6
7
H
I
N
O
S
X
Z
-
-
43
-
-
25
-
8
9
5
6
1
6
8
-
-
4+3
-
-
2+5
7
H
I
N
O
S
X
Z
-
-
7
-
-
7
8
9
14
15
19
24
26
7
H
I
N
O
S
X
Z
-
-
7
-
-
7

 

 

 

 

A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

THE

FAR YONDER SCRIBE

AND OFT TIMES SHADOWED SUBSTANCES WATCHED IN SOME AMAZE

THE

ZED ALIZ ZED

IN

SWIFT REPEAT SCATTER STAR DUST AMONGST THE LETTERS OF THEIR PROGRESS

 

 

NUMBER

9

THE SEARCH FOR THE SIGMA CODE

Cecil Balmond 1998

Cycles and Patterns

Page 165

Patterns

"The essence of mathematics is to look for patterns.

Our minds seem to be organised to search for relationships and sequences. We look for hidden orders.

These intuitions seem to be more important than the facts themselves, for there is always the thrill at finding something, a pattern, it is a discovery - what was unknown is now revealed. Imagine looking up at the stars and finding the zodiac!

Searching out patterns is a pure delight.

Suddenly the counters fall into place and a connection is found, not necessarily a geometric one, but a relationship between numbers, pictures of the mind, that were not obvious before. There is that excitement of finding order in something that was otherwise hidden.

And there is the knowledge that a huge unseen world lurks behind the facades we see of the numbers themselves."

 

 

-
ALL IS NUMBER
-
-
-
3
ALL
25
7
7
2
IS
28
10
1
6
NUMBER
73
28
1
11
ALL IS NUMBER
126
45
9
1+1
-
1+2+6
4+5
-
2
ALL IS NUMBER
9
9
9

 

 

-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
5
9
-
-
-
1
-
-
-
-
-
5
-
-
-
-
-
+
=
20
2+0
=
2
=
2
=
2
-
-
-
14
9
-
-
-
19
-
-
-
-
-
14
-
-
-
-
-
+
=
56
5+6
=
11
1+1
2
=
2
-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
3
-
-
4
5
9
-
1
3
-
3
1
-
7
3
1
7
5
+
=
52
5+2
=
7
=
7
=
7
-
-
21
-
-
22
5
18
-
1
12
-
12
1
-
7
21
1
7
5
+
=
133
1+3+3
=
7
=
7
=
7
-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
21
14
9
22
5
18
19
1
12
-
12
1
14
7
21
1
7
5
+
=
189
1+8+9
=
18
1+8
9
=
9
-
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
+
=
72
7+2
=
9
=
9
=
9
-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-`
-
-
-
-
1
1
-
-
-`
1
-
-
-
1
-
-
-
-
1
occurs
x
4
=
4
=
4
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
3
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
4
=
12
1+2
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
5
-
-
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
2
=
14
1+4
5
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
2
=
18
1+8
9
16
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
29
-
-
17
-
72
-
27
1+6
1+7
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2+9
-
-
1+7
-
7+2
-
2+7
7
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
11
-
-
8
-
9
-
9
-
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
-
-
1+1
-
-
-
-
-
-
-
7
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
2
-
-
8
-
9
-
9

 

 

17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
5
9
-
-
-
1
-
-
-
-
-
5
-
-
-
-
-
+
=
20
2+0
=
2
=
2
=
2
-
-
14
9
-
-
-
19
-
-
-
-
-
14
-
-
-
-
-
+
=
56
5+6
=
11
1+1
2
=
2
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
3
-
-
4
5
9
-
1
3
-
3
1
-
7
3
1
7
5
+
=
52
5+2
=
7
=
7
=
7
-
21
-
-
22
5
18
-
1
12
-
12
1
-
7
21
1
7
5
+
=
133
1+3+3
=
7
=
7
=
7
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
21
14
9
22
5
18
19
1
12
-
12
1
14
7
21
1
7
5
+
=
189
1+8+9
=
18
1+8
9
=
9
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
+
=
72
7+2
=
9
=
9
=
9
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-`
-
-
-
-
1
1
-
-
-`
1
-
-
-
1
-
-
-
-
1
occurs
x
4
=
4
=
4
-
3
-
-
-
-
-
-
-
3
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
4
=
12
1+2
3
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
5
-
-
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
2
=
18
1+8
9
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
29
-
-
17
-
72
-
27
1+7
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2+9
-
-
1+7
-
7+2
-
2+7
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
11
-
-
8
-
9
-
9
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
-
-
1+1
-
-
-
-
-
-
-
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
2
-
-
8
-
9
-
9

 

 

-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
1
-
5
-
-
-
-
-
+
=
15
1+5
=
6
=
6
=
6
-
-
-
-
-
-
9
19
-
14
-
-
-
-
-
+
=
42
4+2
=
6
=
6
=
6
-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
3
3
-
-
-
-
-
3
4
2
5
9
+
=
30
3+0
=
3
=
3
=
3
-
-
1
12
12
-
-
-
-
-
21
13
2
5
18
+
=
84
8+4
=
12
1+2
3
=
3
-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
12
12
-
9
19
-
14
21
13
2
5
18
+
=
126
1+2+6
=
9
=
9
=
9
-
-
1
3
3
-
9
1
-
5
3
4
2
5
9
+
=
45
4+5
=
9
=
9
=
9
-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
1
-
-
-
-
-
-
-
-
-
1
occurs
x
2
=
2
=
2
-
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
3
3
-
-
-
-
-`
3
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
-
-
-
-
-
-
5
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
21
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
24
-
-
11
-
45
-
27
2+1
1+1
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
2+4
-
-
1+1
-
4+5
-
2+7
3
2
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
6
-
-
2
-
9
-
9

 

 

11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
1
-
5
-
-
-
-
-
+
=
15
1+5
=
6
=
6
=
6
-
-
-
-
-
9
19
-
14
-
-
-
-
-
+
=
42
4+2
=
6
=
6
=
6
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
1
3
3
-
-
-
-
-
3
4
2
5
9
+
=
30
3+0
=
3
=
3
=
3
-
1
12
12
-
-
-
-
-
21
13
2
5
18
+
=
84
8+4
=
12
1+2
3
=
3
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
1
12
12
-
9
19
-
14
21
13
2
5
18
+
=
126
1+2+6
=
9
=
9
=
9
-
1
3
3
-
9
1
-
5
3
4
2
5
9
+
=
45
4+5
=
9
=
9
=
9
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
1
-
-
-
-
-
-
-
-
-
1
occurs
x
2
=
2
=
2
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
3
3
-
-
-
-
-`
3
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
-
-
-
-
-
5
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
-
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
24
-
-
11
-
45
-
27
1+1
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
2+4
-
-
1+1
-
4+5
-
2+7
2
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
6
-
-
2
-
9
-
9

 

 

-
ALL IS NUMBER
-
-
-
3
ALL
25
7
7
2
IS
28
10
1
6
NUMBER
73
28
1
11
ALL IS NUMBER
126
45
9
1+1
-
1+2+6
4+5
-
2
ALL IS NUMBER
9
9
9

 

 

9
A
B
C
D
E
F
G
H
I
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
+
=
17
1+7
=
8
-
8
-
-
-
-
-
-
-
-
8
9
+
=
17
1+7
=
8
-
8
9
A
B
C
D
E
F
G
H
I
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
+
=
28
2+8
=
10
1+0
1
-
1
2
3
4
5
6
7
-
-
+
=
28
2+8
=
10
1+0
1
9
A
B
C
D
E
F
G
H
I
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
+
=
45
4+5
=
9
-
9
-
1
2
3
4
5
6
7
8
9
+
=
45
4+5
=
9
-
9
9
A
B
C
D
E
F
G
H
I
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
+
=
1
occurs
x
1
=
1
-
-
2
-
-
-
-
-
-
-
+
=
2
occurs
x
2
=
2
-
-
-
3
-
-
-
-
-
-
+
=
3
occurs
x
3
=
3
-
-
-
-
4
-
-
-
-
-
+
=
4
occurs
x
4
=
4
-
-
-
-
-
5
-
-
-
-
+
=
5
occurs
x
5
=
5
-
-
-
-
-
-
6
-
-
-
+
=
6
occurs
x
6
=
6
-
-
-
-
-
-
-
7
-
-
+
=
7
occurs
x
7
=
7
-
-
-
-
-
-
-
-
8
-
+
=
8
occurs
x
8
=
8
-
-
-
-
-
-
-
-
-
9
+
=
9
occurs
x
9
=
9
9
A
B
C
D
E
F
G
H
I
-
-
45
-
-
45
-
45
-
-
-
-
-
-
-
-
-
9
-
-
4+5
-
-
4+5
-
4+5
9
A
B
C
D
E
F
G
H
I
-
-
9
-
-
9
-
9
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
9
A
B
C
D
E
F
G
H
I
-
-
9
-
-
9
-
9

 

 

9
J
K
L
M
N
O
P
Q
R
-
-
-
-
-
-
-
-
-
-
-
-
-
5
6
-
-
-
+
=
11
1+1
=
2
-
2
-
-
-
-
-
14
15
-
-
-
+
=
11
1+7
=
2
-
2
9
J
K
L
M
N
O
P
Q
R
-
-
-
-
-
-
-
-
-
1
2
3
4
-
-
7
8
9
+
=
34
3+4
=
7
-
7
-
10
11
12
13
-
-
16
17
18
+
=
97
9+7
=
16
1+6
7
9
J
K
L
M
N
O
P
Q
R
-
-
-
-
-
-
-
-
-
10
11
12
13
14
15
16
17
18
+
=
126
1+2+6
=
9
-
9
9
1
2
3
4
5
6
7
8
9
+
=
45
4+5
=
9
-
9
-
J
K
L
M
N
O
P
Q
R
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
+
=
1
occurs
x
1
=
1
-
-
2
-
-
-
-
-
-
-
+
=
2
occurs
x
2
=
2
-
-
-
3
-
-
-
-
-
-
+
=
3
occurs
x
3
=
3
-
-
-
-
4
-
-
-
-
-
+
=
4
occurs
x
4
=
4
-
-
-
-
-
5
-
-
-
-
+
=
5
occurs
x
5
=
5
-
-
-
-
-
-
6
-
-
-
+
=
6
occurs
x
6
=
6
-
-
-
-
-
-
-
7
-
-
+
=
7
occurs
x
7
=
7
-
-
-
-
-
-
-
-
8
-
+
=
8
occurs
x
8
=
8
-
-
-
-
-
-
-
-
-
9
+
=
9
occurs
x
9
=
9
9
J
K
L
M
N
O
P
Q
R
-
-
45
-
-
45
-
45
-
-
-
-
-
-
-
-
-
9
-
-
4+5
-
-
4+5
-
4+5
9
J
K
L
M
N
O
P
Q
R
-
-
9
-
-
9
-
9
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
9
J
K
L
M
N
O
P
Q
R
-
-
9
-
-
9
-
9

 

 

8
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
1
-
-
-
-
6
-
8
+
=
15
1+5
=
6
-
6
-
19
-
-
-
-
24
-
26
+
=
69
6+9
=
15
-
6
8
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
2
3
4
5
-
7
-
+
=
21
2+1
=
3
-
3
-
-
20
21
22
23
-
25
-
+
=
111
1+1+1
=
3
-
3
8
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
19
20
21
22
23
24
25
26
+
=
180
1+8+0
=
9
-
9
-
1
2
3
4
5
6
7
8
+
=
36
3+6
=
9
-
9
8
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
1
=
1
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
2
=
2
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
3
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
4
=
4
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
5
=
5
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
6
=
6
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
7
=
7
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
8
=
8
8
S
T
U
V
W
X
Y
Z
-
-
36
-
-
36
-
36
-
-
-
-
-
-
-
-
-
-
-
3+6
-
-
3+6
-
3+6
8
S
T
U
V
W
X
Y
Z
-
-
9
-
-
9
-
9
-
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
8
S
T
U
V
W
X
Y
Z
-
-
9
-
-
9
-
9

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
9
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-

 

 

-
ALL IS NUMBER
-
-
-
3
ALL
25
7
7
2
IS
28
10
1
6
NUMBER
73
28
1
11
ALL IS NUMBER
126
45
9
1+1
-
1+2+6
4+5
-
2
ALL IS NUMBER
9
9
9

 

 

THE CITY OF REVELATION

John Michell 1972

Gnostic Numbers 

Page 118

"Exactly how they came by their science of numbers is not certain, but they appear to have made the discovery that the numerical code of the Hebrew cabala and those of other mystical systems throughout the world were all degenerate versions of the same once universal system of knowledge that returns within the reach of human perception at certain intervals in time. As the revealed books of the Old Testament were written in a code to be interpreted by reference to number, so were the revelations of the gnostic prophets expressed in words and phrases formed on a system of proportion, which gave life and power to the Christian myth, while allowing initiates to gain a further understanding of the balance of forces that produce the world of phenomena."  

Page 121 / How it was ever supposed that the Hebrew alphabet of twenty- two letters, together with various geometrical symbols might serve to represent the entire moving pattern of the universe is not now easy to understand; but, since all ancient philosophy, religion, magic, the arts and sciences were based on the concept of a correspondence between numbers and cosmic law, it is impossible to appreciate the history of the past without some actual experience of the fundamental truth behind this approach to cosmology. Plato gives a remarkable account in Cratylos of the origin of language and letters. The philosopher is asked whether there is any particular significance in names, for surely they are simply a matter of convention and one is more or less as good as another. After all, foreigners call things by different names and appear to manage just as well as the Greeks in this respect. The answer given is that despite appearances the matter is by no means so simple. Words are the tools of expression, and the making of these, as of any other tools, is the task of a skilled craftsman, in this case the lawgiver. Language has grown corrupt over the ages, and names have deviated from their original perfect forms, which are those used by the gods. But all names were originally formed on certain principles, through knowledge of which it is possible to discover the archetypal meaning of words in current use. 'So perhaps the man who knows about names considers their value and is not confused if some letter is added, transposed or subtracted, or even if the force of the name is expressed in quite different letters.' This is Plato's clearest reference to the mystical science of the cabala, in which letters, words and whole phrases may be substituted for others of the same numerical value. The force of a name is to be found in its number, and can be expressed through any combination of letters, provided the sum of the letters amounts to the appropriate number by gematria.

 

THE MAGIC ALPHABET

 

A
=
1
-
9
ABCDEFGHI
45
45
45
-
-
-
-
-
-
-
-
-
-
J
=
1
-
9
JKLMNOPQR
126
45
45
-
-
-
-
-
-
-
-
-
-
S
=
1
-
8
STUVWXYZ
180
45
36
-
-
-
-
-
-
-
-
-
-
-
-
-
-
351
135
126
-
1
2
3
4
5
6
7
8
9
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
B
=
2
2
1
B
2
2
2
-
-
2
-
-
-
-
-
-
-
C
=
3
3
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
D
=
4
4
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
5
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
6
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
G
=
7
7
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
9
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
45
-
-
-
45
45
45
-
-
-
-
-
-
-
-
-
-
J
=
1
10
1
J
10
1
1
-
1
-
-
-
-
-
-
-
-
K
=
2
11
1
K
11
2
2
-
-
2
-
-
-
-
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
M
=
4
13
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
N
=
5
14
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
15
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
P
=
7
16
1
P
16
7
7
-
-
-
-
-
-
-
7
-
-
Q
=
8
17
1
Q
17
8
8
-
-
-
-
-
-
-
-
8
-
R
=
9
18
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
45
-
-
-
126
45
45
-
-
-
-
-
-
-
-
-
-
S
=
1
19
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
T
=
2
20
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
U
=
3
21
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
V
=
4
22
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
W
=
5
23
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
X
=
6
24
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
25
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
Z
=
8
26
1
Z
26
8
8
-
-
-
-
-
-
-
-
8
-
36
-
-
-
180
45
36
-
-
-
-
-
-
-
-
-
-
126
-
-
-
-
-
-
-
3
6
9
12
15
18
21
24
18
-
-
1+2+6
-
9
ABCDEFGHI
45
45
45
-
-
-
-
1+2
1+5
1+8
2+1
2+4
1+8
-
-
9
-
9
JKLMNOPQR
126
45
45
-
3
6
9
3
6
9
3
6
9
-
-
-
-
8
STUVWXYZ
180
45
36
-
-
-
-
-
-
-
-
-
-
-
-
9
-
26
ADD TO REDUCE
351
135
126
-
3
6
9
3
6
9
3
6
9
-
-
-
-
2+6
REDUCE TO DEDUCE
3+5+1
1+3+5
1+2+6
-
-
-
-
-
-
-
-
-
-
-
-
9
-
8
ESSENCE OF NUMBER
9
9
9
-
3
6
9
3
6
9
3
6
9

 

 

A
=
1
-
9
ABCDEFGHI
45
45
45
-
-
-
-
-
-
-
-
-
-
J
=
1
-
9
JKLMNOPQR
126
45
45
-
-
-
-
-
-
-
-
-
-
S
=
1
-
8
STUVWXYZ
180
45
36
-
-
-
-
-
-
-
-
-
-
-
-
-
-
351
135
126
-
1
2
3
4
5
6
7
8
9
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
B
=
2
2
1
B
2
2
2
-
-
2
-
-
-
-
-
-
-
C
=
3
3
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
D
=
4
4
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
5
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
6
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
G
=
7
7
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
9
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
J
=
1
10
1
J
10
1
1
-
1
-
-
-
-
-
-
-
-
K
=
2
11
1
K
11
2
2
-
-
2
-
-
-
-
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
M
=
4
13
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
N
=
5
14
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
15
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
P
=
7
16
1
P
16
7
7
-
-
-
-
-
-
-
7
-
-
Q
=
8
17
1
Q
17
8
8
-
-
-
-
-
-
-
-
8
-
R
=
9
18
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
S
=
1
19
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
T
=
2
20
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
U
=
3
21
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
V
=
4
22
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
W
=
5
23
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
X
=
6
24
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
25
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
Z
=
8
26
1
Z
26
8
8
-
-
-
-
-
-
-
-
8
-
126
-
-
-
-
-
-
-
3
6
9
12
15
18
21
24
18
-
-
1+2+6
-
9
ABCDEFGHI
45
45
45
-
-
-
-
1+2
1+5
1+8
2+1
2+4
1+8
-
-
9
-
9
JKLMNOPQR
126
45
45
-
3
6
9
3
6
9
3
6
9
-
-
-
-
8
STUVWXYZ
180
45
36
-
-
-
-
-
-
-
-
-
-
-
-
9
-
26
ADD TO REDUCE
351
135
126
-
3
6
9
3
6
9
3
6
9
-
-
-
-
2+6
REDUCE TO DEDUCE
3+5+1
1+3+5
1+2+6
-
-
-
-
-
-
-
-
-
-
-
-
9
-
8
ESSENCE OF NUMBER
9
9
9
-
3
6
9
3
6
9
3
6
9

 

 

A
=
1
-
9
ABCDEFGHI
45
45
45
-
-
-
-
-
-
-
-
-
-
J
=
1
-
9
JKLMNOPQR
126
45
45
-
-
-
-
-
-
-
-
-
-
S
=
1
-
8
STUVWXYZ
180
45
36
-
-
-
-
-
-
-
-
-
-
-
-
-
-
351
135
126
-
1
2
3
4
5
6
7
8
9
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
J
=
1
10
1
J
10
1
1
-
1
-
-
-
-
-
-
-
-
S
=
1
19
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
B
=
2
2
1
B
2
2
2
-
-
2
-
-
-
-
-
-
-
K
=
2
11
1
K
11
2
2
-
-
2
-
-
-
-
-
-
-
T
=
2
20
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
C
=
3
3
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
U
=
3
21
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
D
=
4
4
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
M
=
4
13
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
V
=
4
22
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
5
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
14
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
W
=
5
23
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
6
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
15
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
X
=
6
24
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
G
=
7
7
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
P
=
7
16
1
P
16
7
7
-
-
-
-
-
-
-
7
-
-
Y
=
7
25
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
Q
=
8
17
1
Q
17
8
8
-
-
-
-
-
-
-
-
8
-
Z
=
8
26
1
Z
26
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
9
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
R
=
9
18
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
126
-
-
-
-
-
-
-
3
6
9
12
15
18
21
24
18
-
-
1+2+6
-
9
ABCDEFGHI
45
45
45
-
-
-
-
1+2
1+5
1+8
2+1
2+4
1+8
-
-
9
-
9
JKLMNOPQR
126
45
45
-
3
6
9
3
6
9
3
6
9
-
-
-
-
8
STUVWXYZ
180
45
36
-
-
-
-
-
-
-
-
-
-
-
-
9
-
26
ADD TO REDUCE
351
135
126
-
3
6
9
3
6
9
3
6
9
-
-
-
-
2+6
REDUCE TO DEDUCE
3+5+1
1+3+5
1+2+6
-
-
-
-
-
-
-
-
-
-
-
-
9
-
8
ESSENCE OF NUMBER
9
9
9
-
3
6
9
3
6
9
3
6
9

 

 

LETTERS TRANSPOSED INTO NUMBER

RE-ARRANGED IN NUMERICAL ORDER

 

S
=
1
-
8
STUVWXYZ
180
36
36
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
S
=
1
19
1
S
19
1
1
-
1
-
-
-
-
-
-
-
-
T
=
2
20
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
U
=
3
21
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
V
=
4
22
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
W
=
5
23
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
X
=
6
24
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
25
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
Z
=
8
26
1
Z
26
8
8
-
-
-
-
-
-
-
-
8
-
36
-
8
STUVWXYZ
180
36
36
-
1
2
3
4
5
6
7
8
9
-
-
3+6
-
-
-
1+8+0
3+6
3+6
-
-
-
-
-
-
-
-
-
-
-
-
9
-
8
STUVWXYZ
9
9
9
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
8
STUVWXYZ
9
9
9
-
1
2
3
4
5
6
7
8
9

 

STUVWXYZ 180 ZYXWVUTS

STUVWXYZ 36 ZYXWVUTS

STUVWXYZ 9 ZYXWVUTS

 

 

JUST SIX NUMBERS

Martin Rees

1
999

OUR COSMIC HABITAT

PLANETS STARS AND LIFE

Page 24

A

proton

is

1,836 times heavier than an electron, and the number 1,836

would have the same connotations to any 'intelligence'

Page 24 / 25
"A manifestly artificial signal- even if it were as boring as lists of prime numbers, or the digits of 'pi' - would imply that 'intelli- gence' wasn't unique to the Earth and had evolved elsewhere. The nearest potential sites are so far away that signals would take many years in transit. For this reason alone, transmission would be primarily one-way. There would be time to send a measured response, but no scope for quick repartee!
Any remote beings who could communicate with us would have some concepts of mathematics and logic that paralleled our own. And they would also share a knowledge of the basic particles and forces that govern our universe. Their habitat may be very different (and the biosphere even more different) from ours here on Earth; but they, and their planet, would be made of atoms just like those on Earth. For them, as for us, the most important particles would be protons and electrons: one electron orbiting a proton makes a hydrogen atom, and electric currents and radio transmitters involve streams of electrons. A proton is 1,836 times heavier than an electron, and the number 1,836 would have the same connotations to any 'intelligence' "able and motivated to transmit radio signals. All the basic forces and natural laws would be the same. Indeed, this uniformity - without which our universe would be a far more baffling place - seems to extend to the remotest galaxies that astronomers can study. (Later chapters in this book will, however, speculate about other 'universes', forever beyond range of our telescopes, where different laws may prevail.)
Clearly, alien beings wouldn't use metres, kilograms or seconds. But we could exchange information about the ratios of two masses (such as thc ratio of proton and electron masses) or of two lengths, which are 'pure numbers' that don't depend on what units are used: the statement that one rod is ten times as long as another is true (or false) whether we measure lengths / in feet or metres or some alien units

 

A

proton

is

1,836 times heavier than an electron, and the number 1,836

would have the same connotations to any 'intelligence'

 

E
=
5
-
8
EIGHTEEN
73
46
1
T
=
2
-
9
THIRTYSIX
152
53
8
-
-
7
4
17
First Total
225
99
9
-
-
-
-
1+7
Add to Reduce
2+2+5
9+9
-
Q
-
7
-
8
Second Total
9
18
9
-
-
-
-
-
Reduce to Deduce
-
1+8
-
Q
-
7
-
8
Essence of Number
9
9
9

 

 

3
SUN
54
9
9
5
EARTH
52
25
7
4
MOON
57
21
3
12
First Total
163
55
19
1+2
Add to Reduce
1+6+3
5+5
6+2
3
Second Total
10
10
10
-
Reduce to Deduce
1+0
1+0
1+0
3
Essence of Number
1
1
1

 

THERE IS NO ATTEMPT MADE TO DESCRIBE THE CREATIVE PROCESS REALISTICALLY

THE ACCOUNT IS SYMBOLIC AND SHOWS GOD CREATING THE WORLD BY MEANS OF LANGUAGE

AS THOUGH WRITING A BOOK BUT LANGUAGE ENTIRELY TRANSFORMED

THE MESSAGE OF CREATION IS CLEAR EACH LETTER OF

THE

ALPHABET

IS

GIVEN

A

NUMERICAL

VALUE BY COMBINING THE LETTERS WITH THE SACRED NUMBERS

REARRANGING THEM IN ENDLESS CONFIGURATIONS

THE MYSTIC WEANED THE MIND AWAY FROM THE NORMAL CONNOTATIONS OF WORDS

 

 

 

-
THE RAINBOW LIGHT
-
-
-
3
THE
33
15
6
7
RAINBOW
82
37
1
5
LIGHT
56
29
2
15
THE RAINBOW LIGHT
171
81
9
1+5
-
1+7+1
8+1
-
6
THE RAINBOW LIGHT
9
9
9

 

 

3
3
-
A+B+C
6
6
6
2
-
2
D+E
9
9
9
3
3
-
F+G+H
21
21
3
1
-
1
I
9
9
9
3
3
-
J+K+L
33
6
6
2
-
2
M+N
27
9
9
2
2
-
O+P
31
13
4
3
-
3
QRS
54
18
9
3
-
3
TUV
63
9
9
3
-
3
WXY
72
18
9
1
1
-
Z
26
8
8
26
12
14
First Total
351
126
81
2+6
1+2
1+4
Add to Reduce
3+5+1
1+2+6
8+1
8
3
5
Reduce to Deduce
9
9
9

 

 

3
A+B+C
6
6
6
-
D+E
-
-
-
3
F+G+H
21
21
3
-
I
-
-
-
3
J+K+L
33
6
6
-
M+N
-
-
-
2
O+P
31
13
4
-
QRS
-
-
-
-
TUV
-
-
-
-
WXY
-
-
-
1
Z
26
8
8
12
First Total
117
54
27
2+6
Add to Reduce
1+1+7
5+4
2+7
8
Reduce to Deduce
9
9
9

 

 

-
A+B+C
-
-
-
2
D+E
9
9
9
-
F+G+H
-
-
-
1
I
9
9
9
-
J+K+L
-
-
-
2
M+N
27
9
9
-
O+P
-
-
-
3
QRS
54
18
9
3
TUV
63
9
9
3
WXY
72
18
9
-
Z
-
-
-
14
First Total
234
72
54
1+4
Add to Reduce
2+3+4
7+2
5+4
5
Reduce to Deduce
9
9
9

 

 

4

ZERO

64

28

1
3

ONE
34
16
7
3

TWO
58
13
4
5

THREE
56
29
2
4

FOUR
60
24
6
4

FIVE
42
24
6
3

SIX
52
16
7
5

SEVEN
65
20
2
5

EIGHT
49
31
4
4

NINE
42
24
6
40
-
522
225
45
4+0
-
5+2+2
2+2+5
4+5
4
-
9
9
9

 

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

0
-
Z
=
8
1
4
ZERO
64
28
1
1
-
O
=
6
2
3
ONE
34
16
7
2
-
T
=
2
3
3
TWO
58
13
4
3
-
T
=
2
4
5
THREE
56
29
2
4
-
F
=
6
5
4
FOUR
60
24
6
5
-
F
=
6
6
4
FIVE
42
24
6
6
-
S
=
1
7
3
SIX
52
16
7
7
-
S
=
1
8
5
SEVEN
65
20
2
8
-
E
=
5
9
5
EIGHT
49
31
4
9
-
N
=
5
10
4
NINE
42
24
6
45
-
-
-
42
-
40
Add
522
225
45
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
9
-
-
-
6
-
4
Deduce
9
9
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
3
-
5
-
-
8
9
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
3
-
5
-
7
8
9
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
3
4
5
-
-
8
9
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
3
-
5
-
-
8
9
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
3
-
5
6
-
8
9
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
3
-
5
6
-
8
9
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
3
-
5
-
7
8
9
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
3
-
5
-
-
8
9
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
3
4
5
-
-
8
9
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
3
-
5
6
-
8
9
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
4
6
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
7
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
4
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
6
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
6
-
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
7
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
4
-
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
6
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
8
18
14
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
1+8
1+4
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
8
9
5

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
3
-
5
-
-
8
9
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
3
-
5
-
-
8
9
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
3
-
5
-
-
8
9
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
3
4
5
-
-
8
9
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
3
4
5
-
-
8
9
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
3
-
5
6
-
8
9
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
3
-
5
6
-
8
9
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
3
-
5
6
-
8
9
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
3
-
5
-
7
8
9
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
3
-
5
-
7
8
9
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
4
6
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
4
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
4
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
6
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
6
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
6
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
7
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
7
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
8
18
14
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
1+8
1+4
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
8
9
5

 

 

1
-
O
=
6
1
3
ONE
34
16
7
2
-
T
=
2
2
3
TWO
58
13
4
3
-
T
=
2
3
5
THREE
56
29
2
4
-
F
=
6
4
4
FOUR
60
24
6
5
-
F
=
6
5
4
FIVE
42
24
6
6
-
S
=
1
6
3
SIX
52
16
7
7
-
S
=
1
7
5
SEVEN
65
20
2
8
-
E
=
5
8
5
EIGHT
49
31
4
9
-
N
=
5
9
4
NINE
42
24
6
45
-
-
-
34
-
36
Add
458
197
44
4+5
-
-
-
3+4
4
3+6
Reduce
4+5+8
1+9+7
4+4
9
-
-
-
7
4
9
Deduce
17
17
8
-
-
-
-
-
-
-
Produce
1+7
1+7
-
9
-
-
-
7
-
9
Essence
8
8
8

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
O
=
6
1
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
2
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
3
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
4
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
5
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
6
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
7
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
8
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
9
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
34
-
36
Add
458
197
44
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
3+4
-
3+6
Reduce
4+5+8
1+9+7
4+4
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
7
4
9
Deduce
17
17
8
-
1
4
3
8
5
18
14
8
9
-
-
-
-
-
-
-
Produce
1+7
1+7
-
-
-
-
-
-
-
-
-
-
-
9
-
-
-
7
-
9
Essence
8
8
8
-
1
4
3
8
5
9
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
O
=
6
1
3
ONE
34
16
7
-
1
-
3
-
5
-
7
8
9
2
-
T
=
2
2
3
TWO
58
13
4
-
1
-
3
4
5
-
-
8
9
3
-
T
=
2
3
5
THREE
56
29
2
-
1
2
3
-
5
-
-
8
9
4
-
F
=
6
4
4
FOUR
60
24
6
-
1
-
3
-
5
6
-
8
9
5
-
F
=
6
5
4
FIVE
42
24
6
-
1
-
3
-
5
6
-
8
9
6
-
S
=
1
6
3
SIX
52
16
7
-
1
-
3
-
5
-
7
8
9
7
-
S
=
1
7
5
SEVEN
65
20
2
-
1
2
3
-
5
-
-
8
9
8
-
E
=
5
8
5
EIGHT
49
31
4
-
1
-
3
4
5
-
-
8
9
9
-
N
=
5
9
4
NINE
42
24
6
-
1
-
3
-
5
6
-
8
9
45
-
-
-
34
-
36
Add
458
197
44
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
3+4
-
3+6
Reduce
4+5+8
1+9+7
4+4
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
7
4
9
Deduce
17
17
8
-
1
4
3
8
5
18
14
8
9
-
-
-
-
-
-
-
Produce
1+7
1+7
-
-
-
-
-
-
-
-
-
-
-
9
-
-
-
7
-
9
Essence
8
8
8
-
1
4
3
8
5
9
5
8
9

 

 

0
-
4
ZERO
8
5
9
6
-
=
28
2+8
=
10
1+0
1
1
-
3
ONE
6
5
5
-
-
=
16
1+6
=
7
-
7
2
-
3
TWO
2
5
6
-
-
=
13
1+3
=
4
-
4
3
-
5
THREE
2
8
9
5
5
=
29
2+9
=
11
1+1
2
4
-
4
FOUR
6
6
3
9
-
=
24
2+4
=
6
-
6
5
-
4
FIVE
6
9
4
5
-
=
24
2+4
=
6
-
6
6
-
3
SIX
1
9
6
-
-
=
16
1+6
=
7
-
7
7
-
5
SEVEN
1
5
4
5
5
=
20
2+0
=
2
-
2
8
-
5
EIGHT
5
9
7
8
2
=
31
3+1
=
4
-
4
9
-
4
NINE
5
9
5
5
-
=
24
2+4
=
6
-
6
45
-
40
Add
42
70
58
43
12
-
225
-
-
63
-
45
4+5
-
4+0
-
4+2
7+0
5+8
4+3
1+2
-
2+2+5
-
-
6+3
-
4+5
9
-
4
Reduce
6
7
13
7
3
-
9
-
-
9
-
-
-
-
-
-
-
-
1+3
-
-
-
-
-
-
-
-
-
9
-
4
Deduce
6
7
4
7
3
-
9
-
-
9
-
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
1
-
F
=
6
2
5
FIRST
72
27
9
-
-
-
-
-
-
-
-
-
9
2
-
S
=
1
3
6
SECOND
60
24
6
-
-
-
-
-
-
6
-
-
-
3
-
T
=
2
4
5
THIRD
59
32
5
-
-
-
-
-
5
-
-
-
-
4
-
F
=
6
5
6
FOURTH
88
34
7
-
-
-
-
-
-
-
7
-
-
5
-
F
=
6
6
5
FIFTH
49
31
4
-
-
-
-
4
-
-
-
-
-
6
-
S
=
1
7
5
SIXTH
80
26
8
-
-
-
-
-
-
-
-
8
-
7
-
S
=
1
8
7
SEVENTH
93
30
3
-
-
-
3
-
-
-
-
-
-
8
-
E
=
5
9
6
EIGHTH
57
39
3
-
-
-
3
-
-
-
-
-
-
9
-
N
=
5
10
5
NINTH
65
29
2
-
-
2
-
-
-
-
-
-
-
45
-
-
-
41
-
54
Add
687
300
48
-
1
2
6
4
5
6
7
8
9
4+5
-
-
-
4+1
-
5+4
Reduce
6+8+7
3+0+0
4+8
-
-
-
-
-
-
-
-
-
-
9
-
-
-
5
-
9
Deduce
21
3
12
-
1
2
6
4
5
6
7
8
9
-
-
-
-
-
-
-
Reduce
2+1
-
1+2
-
-
-
-
-
-
-
-
-
-
9
-
-
-
5
-
9
Essence
3
3
3
-
1
2
6
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
9
-
N
=
5
10
5
NINTH
65
29
2
-
-
2
-
-
-
-
-
-
-
7
-
S
=
1
8
7
SEVENTH
93
30
3
-
-
-
3
-
-
-
-
-
-
8
-
E
=
5
9
6
EIGHTH
57
39
3
-
-
-
3
-
-
-
-
-
-
5
-
F
=
6
6
5
FIFTH
49
31
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
4
5
THIRD
59
32
5
-
-
-
-
-
5
-
-
-
-
2
-
S
=
1
3
6
SECOND
60
24
6
-
-
-
-
-
-
6
-
-
-
4
-
F
=
6
5
6
FOURTH
88
34
7
-
-
-
-
-
-
-
7
-
-
6
-
S
=
1
7
5
SIXTH
80
26
8
-
-
-
-
-
-
-
-
8
-
1
-
F
=
6
2
5
FIRST
72
27
9
-
-
-
-
-
-
-
-
-
9
45
-
-
-
41
-
54
Add
687
300
48
-
1
2
6
4
5
6
7
8
9
4+5
-
-
-
4+1
-
5+4
Reduce
6+8+7
3+0+0
4+8
-
-
-
-
-
-
-
-
-
-
9
-
-
-
5
-
9
Deduce
21
3
12
-
1
2
6
4
5
6
7
8
9
-
-
-
-
-
-
-
Reduce
2+1
-
1+2
-
-
-
-
-
-
-
-
-
-
9
-
-
-
5
-
9
Essence
3
3
3
-
1
2
6
4
5
6
7
8
9

 

NUMBERS RE-ARRANGED IN NUMERICAL ORDER

 

Pietro Bongo - Wikipedia

https://en.wikipedia.org/wiki/Pietro_Bongo

Pietro Bongo (alternate spelling: Petrus Bungus) was a medieval Italian writer. ... Bibliography[edit]. Some of his books are: Numerorum Mysteria ...

Pietro Bongo (alternate spelling: Petrus Bungus) was a medieval Italian writer.
He came from a noble family. He was born and raised in Bergamo, Italy.[1]
He died on 24 September 1601.[2]

He studied the four mathematical arts of the quadrivium: arithmetic and geometry, music theory and astronomy, and philosophy and theology, beside the classical poetry and the occult sciences of magic and kabbalah. He mastered the Hebrew, Greek, and Latin languages.[3]
In his books, he has tried his best to reconcile Pythagorean doctrine with Christian theology.[4]

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
N
=
5
-
9
NUMERORUM
138
48
3
-
-
-
-
-
-
-
-
-
-
M
=
4
-
8
MYSTERIA
110
38
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
N
=
5
1
1
N
5
5
5
-
-
-
-
-
5
7
-
-
-
U
=
3
2
1
U
21
3
3
-
-
-
3
-
-
7
-
-
-
M
=
4
3
1
M
13
4
4
-
-
-
-
4
7
-
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
-
5
7
-
-
-
R
=
9
5
1
R
9
9
9
-
-
-
3
-
-
-
-
-
9
O
=
6
6
1
O
15
6
6
-
-
-
-
-
-
6
8
-
-
R
=
9
7
1
R
9
9
9
-
-
-
3
-
-
-
-
-
9
U
=
3
8
1
U
21
3
3
-
-
-
3
-
-
7
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
7
-
-
-
-
-
-
48
9
-
138
48
48
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
M
=
4
10
1
M
13
4
4
-
-
-
-
4
7
-
-
-
-
Y
=
7
11
1
Y
25
7
7
-
-
-
-
-
-
-
7
8
-
S
=
1
12
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
T
=
2
12
1
T
20
2
2
-
-
2
-
-
-
7
-
-
-
E
=
5
13
1
E
5
5
5
-
-
-
-
-
5
7
-
-
-
R
=
9
14
1
R
9
9
9
-
-
-
3
-
-
-
-
-
9
I
=
9
15
1
I
9
9
9
-
-
-
3
-
-
-
-
-
9
A
=
1
16
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
-
-
38
17
-
110
47
38
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
86
4
17
MYSTERIA
110
47
38
-
-
-
-
-
-
-
-
-
-
-
-
8+6
-
1+7
NUMERORUM
138
48
48
-
-
-
-
-
-
-
-
-
-
-
-
14
-
8
First Total
248
95
86
-
2
2
6
12
15
6
7
8
36
-
-
1+4
-
-
Add to Reduce
2+4+8
9+5
8+6
-
-
-
-
1+2
1+5
-
-
-
3+6
-
-
5
-
8
Second Total
14
14
14
-
2
2
6
12
6
6
7
8
9
-
-
-
-
-
Reduce to Produce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
Q
-
5
-
8
Essence of Number
5
5
5
-
2
2
6
3
6
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
N
=
5
-
9
NUMERORUM
138
48
3
-
-
-
-
-
-
-
-
-
-
M
=
4
-
8
MYSTERIA
110
38
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
N
=
5
1
1
N
5
5
5
-
-
-
-
-
5
7
-
-
-
U
=
3
2
1
U
21
3
3
-
-
-
3
-
-
7
-
-
-
M
=
4
3
1
M
13
4
4
-
-
-
-
4
7
-
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
-
5
7
-
-
-
R
=
9
5
1
R
9
9
9
-
-
-
3
-
-
-
-
-
9
O
=
6
6
1
O
15
6
6
-
-
-
-
-
-
6
8
-
-
R
=
9
7
1
R
9
9
9
-
-
-
3
-
-
-
-
-
9
U
=
3
8
1
U
21
3
3
-
-
-
3
-
-
7
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
7
-
-
-
-
M
=
4
10
1
M
13
4
4
-
-
-
-
4
7
-
-
-
-
Y
=
7
11
1
Y
25
7
7
-
-
-
-
-
-
-
7
8
-
S
=
1
12
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
T
=
2
12
1
T
20
2
2
-
-
2
-
-
-
7
-
-
-
E
=
5
13
1
E
5
5
5
-
-
-
-
-
5
7
-
-
-
R
=
9
14
1
R
9
9
9
-
-
-
3
-
-
-
-
-
9
I
=
9
15
1
I
9
9
9
-
-
-
3
-
-
-
-
-
9
A
=
1
16
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
-
-
86
4
17
MYSTERIA
110
47
38
-
-
-
-
-
-
-
-
-
-
-
-
8+6
-
1+7
NUMERORUM
138
48
48
-
-
-
-
-
-
-
-
-
-
-
-
14
-
8
First Total
248
95
86
-
2
2
6
12
15
6
7
8
36
-
-
1+4
-
-
Add to Reduce
2+4+8
9+5
8+6
-
-
-
-
1+2
1+5
-
-
-
3+6
-
-
5
-
8
Second Total
14
14
14
-
2
2
6
12
6
6
7
8
9
-
-
-
-
-
Reduce to Produce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
Q
-
5
-
8
Essence of Number
5
5
5
-
2
2
6
3
6
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
N
=
5
-
9
NUMERORUM
138
48
3
-
-
-
-
-
-
-
-
-
-
M
=
4
-
8
MYSTERIA
110
38
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
S
=
1
12
1
S
19
10
1
-
1
-
-
-
-
-
-
8
-
A
=
1
16
1
A
1
1
1
-
1
-
-
-
-
-
-
8
-
T
=
2
12
1
T
20
2
2
-
-
2
-
-
-
7
-
8
-
U
=
3
2
1
U
21
3
3
-
-
-
3
-
-
7
-
8
-
U
=
3
8
1
U
21
3
3
-
-
-
3
-
-
7
-
8
-
M
=
4
3
1
M
13
4
4
-
-
-
-
4
7
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
7
-
-
8
-
M
=
4
10
1
M
13
4
4
-
-
-
-
4
7
-
-
8
-
N
=
5
1
1
N
5
5
5
-
-
-
-
-
5
7
-
8
-
E
=
5
4
1
E
5
5
5
-
-
-
-
-
5
7
-
8
-
E
=
5
13
1
E
5
5
5
-
-
-
-
-
5
7
-
8
-
O
=
6
6
1
O
15
6
6
-
-
-
-
-
-
6
8
8
-
Y
=
7
11
1
Y
25
7
7
-
-
-
-
-
-
-
7
8
-
R
=
9
5
1
R
9
9
9
-
-
-
3
-
-
-
-
8
9
R
=
9
7
1
R
9
9
9
-
-
-
3
-
-
-
-
8
9
R
=
9
14
1
R
9
9
9
-
-
-
3
-
-
-
-
8
9
I
=
9
15
1
I
9
9
9
-
-
-
3
-
-
-
-
8
9
-
-
86
4
17
MYSTERIA
110
47
38
-
-
-
-
-
-
-
-
-
-
-
-
8+6
-
1+7
NUMERORUM
138
48
48
-
-
-
-
-
-
-
-
-
-
-
-
14
-
8
First Total
248
95
86
-
2
2
6
12
15
6
7
8
36
-
-
1+4
-
-
Add to Reduce
2+4+8
9+5
8+6
-
-
-
-
1+2
1+5
-
-
-
3+6
-
-
5
-
8
Second Total
14
14
14
-
2
2
6
12
6
6
7
8
9
-
-
-
-
-
Reduce to Produce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
Q
-
5
-
8
Essence of Number
5
5
5
-
2
2
6
3
6
6
7
8
9

 

 

PLANET EARTH PLANT E PLANT
EARTH THE RA IS.
HEART EARTH TERAH THERA IS

 

18366318

 

LANGUAGE LETTERS TALKING NUMBERS TALKING NUMBERS TALKING LETTERS

 

 

THE CONVERSATION WENT AS FOLLOWS

 

 

SO I SAID

 

 

SO SHE SAID

 

 

WELL I NEVER DID YOU EVER HERE WE R SPEAKING IN TONGUES

 

 

 

 

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = 351 = Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = 126 = Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = 9 = Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

 

 

ABCDEFGH I JKLMNOPQ R STUVWXYZ = 351 = ZYXWVUTS R QPONMLKJ I HGFEDCBA

ABCDEFGH I JKLMNOPQ R STUVWXYZ = 126 = ZYXWVUTS R QPONMLKJ I HGFEDCBA

ABCDEFGH I JKLMNOPQ R STUVWXYZ = 9 = ZYXWVUTS R QPONMLKJ I HGFEDCBA

 

 

MIND BORN SONS, THOSE PATENT PATIENT PATENTED PATTERN MAKERS.
MIND=4 BORN=4 SONS=4 THOSE=4 PATENT=4 PATIENT=4 PATENTED=4 PATTERN=4 MAKERS=4

 

 

Nature's Numbers
Ian Stewart 1995

Numerology is the easiest-and consequently the most dangerous-method for finding patterns. It is easy because anybody can do it and dangerous for the same reason. The difficulty lies in distinguishing significant numerical patterns from accidental ones. Here's a case in point. Kepler was fascinated with patterns in nature, and he devoted much of his life to looking for them in the behaviour of the planets. He devised a simple and tidy theory for the existence of precisely six planets (in his time only Mercury, Venus, Earth, Mars, Jupiter, and Saturn were known). He also discovered a very strange pattern relating the orbital period of a / planet- the time it takes to go once around the Sun-to its distance from the Sun. Recall that the square of a number is what you get when you multiply it by itself: for example, the square of 4 is 4 x 4 = 16. Similarly, the cube is what you get when you multiply it by itself twice: for example, the cube of 4 is 4 x 4 x 4 = 64. Kepler found that if you take the cube of the distance of any planet from the Sun and divide it by the square of its orbital period, you always get the same number. It was not an especially elegant number, but it was the same for all six planets.

Which of these numerological observations is the more significant? The verdict of posterity is that it is the second one, the complicated and rather arbitrary calculation with squares and cubes. This numerical pattern was one of the key steps towards Isaac Newton's theory of gravity, which has explained all sorts of puzzles about the motion of stars and planets. In contrast, Kepler's neat, tidy theory for the number of planets has been buried without trace. For a start it must have been wrong, because we now know of nine planets, not six. There could be even more, farther out from the Sun, and small enough to be undetectable But more important, we no longer expect to find a neat, tidy theory for the number of planets. We think that the Solar System condensed from a cloud of gas surrounding the Sun, and the number of planets presumably depended on the amount of matter in the gas cloud, how it was distributed, and how fast and in what directions it was moving. An equally plausible gas cloud could have given us eight planets, or eleven; the number is accidental, depending on the initial conditions of the gas cloud, rather than universal, reflecting a general law of nature"

Page 6

" The big problem with numerological pattern-seeking is that it generates millions of accidentals for each universal. Nor is it always obvious which is which. For example, there are three stars, roughly equally spaced and in a straight line, in the belt of the constellation Orion. Is that a clue to a significant law of nature?
Here's a similar question. Io, Europa, and Ganymede are three of Jupiter's larger satellites. They orbit the planet in , respectively, 1.77, 3.55, and 7.16 days. Each of these numbers is almost exactly twice the previous one. Is that a significant pattern? Three stars in a row, in terms of orbital period. Which pattern if either, is an important clue..."
    "… In addition to numerical patterns there are geometric ones…"
    "… Until recently the main shapes that appealed to mathematicians were very simple ones: triangles, squares, pen / Page 7 /tagons, hexagons, circles, ellipses, spirals, cubes, spheres, cones, and so on. All of these shapes can be found in nature, although some are far more common, or more evident, than others. The rainbow, for example, is a collection of circles, one for each colour. We don't normally see the entire circle just an arc; but rainbows seen from the air can be complete circles. You also see circles in the ripples on a pond, in the human eye, and on butterflies wings.
         Talking of ripples, the flow of fluids provides an inexhaustible supply of nature's patterns. There are waves of many different kinds-surging toward a beach in parallel ranks, spreading in a V-shape behind a moving boat, radiating outward from an underwater earthquake…"
"…There are swirling spiral whirlpools and tiny vortices. And there is the apparently structureless, random frothing of turbulent flow, one of the great enigmas of mathematics and physics. There are similar patterns in the atmosphere, too, the most dramatic being the vast spiral of a hurricane…"
    "…There are also wave patterns on land. The most strikingly mathematical landscapes on Earth are to be found in the great ergs, or sand oceans, of the Arabian and Sahara deserts. Even when the wind blows steadily in a fixed direction, sand dunes form. The simplest pattern is that of transverse dunes, which-just like ocean waves-line up in parallel straight rows at right angles to the prevailing wind direction. Sometimes the rows themselves become wavy in which case they are called barchanoid ridges; sometimes they break up into / Page 8 / innumerable shield-shaped barchan dunes. If the sand is slightly moist, and there is a little vegetation to bind it together, then you may find parabolic dunes-shaped like a U, with the rounded end pointing in the direction of the wind. These sometimes occur in clusters, and they resemble the teeth of a rake. If the wind direction is variable, other forms become possible. For example, clusters of sand shaped dunes can form, each having several irregular arms radiating from a central peak. They arrange themselves in a random pattern of spots.

Chapter 6

Page 81

"Nature's symmetries can be found on every scale, from the structure of subatomic particles to that of the entire universe. Many chemical molecules are symmetric. The methane molecule is a tetrahedron - a triangular-sided pyramid - with one carbon atom at its center and four hydrogen atoms at its corners Benzene has the sixfold symmetry of a regular hexagon. The fashionable molecule buckminsterfullerene is a truncated icosahedral cage of sixty carbon atoms. (An icosahedron is a regular solid with twenty triangular faces;
"truncated" means that the corners are cut off.) Its symmetry lends it a remarkable stability, which has opened up new possibilities for organic chemistry.
    On a slightly larger scale than molecules, we find symmetries in cellular structure; at the heart of cellular replication lies a tiny piece of mechanical engineering. Deep within each / Page 82  / living cell, there is a rather shapeless structure known as the centrosome, which sprouts long thin microtubules, basic components of the cell's internal "skeleton", like a diminutive sea urchin. Centrsomes were first discovered in 1887 and play an important role in organizing cell division. How-ever in one respect the structure of the centresome is astonishingly symmetric. Inside it has two structures, known as centrioles, positioned at right angles to each other. Each centriole is cylindrical, made from twenty-seven microtubules fused together along their lengths in threes, and arranged with perfect ninefold symmetry. The microtubules themselves also have an astonishingley regular symmetric form. They are hollow tubes, made from a perfect regular checkerboard pattern of units that contain two distinct proteins, alpha- and betatubulin. One day, perhaps, we will understand why nature chose these symmetric forms. But it is amazing to see symmetric structures at the core of a living cell."

 

 

www.merriam-webster.com/dictionary/algorithm

a procedure for solving a mathematical problem (as of finding the greatest common divisor) in a finite number of steps that frequently involves repetition of an ...

algorithm [ˈælgəˌrɪðəm]
n
1. (Mathematics) a logical arithmetical or computational procedure that if correctly applied ensures the solution of a problem Compare heuristic
2. (Mathematics) Logic Maths a recursive procedure whereby an infinite sequence of terms can be generated Also called algorism
[changed from algorism, through influence of Greek arithmos number]
algorithmic adj
aal·go·rithm (lg-rm)
n.
A step-by-step problem-solving procedure, especially an established, recursive computational procedure for solving a problem in a finite number of steps.
algorithmically adv

algorithm (lg-rthm)
A finite set of unambiguous instructions performed in a prescribed sequence to achieve a goal, especially a mathematical rule or procedure used to compute a desired result. Algorithms are the basis for most computer programming.

Noun 1. algorithm - a precise rule (or set of rules) specifying how to solve some problem
algorithmic program, algorithmic rule
formula, rule - (mathematics) a standard procedure for solving a class of mathematical problems; "he determined the upper bound with Descartes' rule of signs"; "he gave us a general formula for attacking polynomials"
sorting algorithm - an algorithm for sorting a list
stemming algorithm, stemmer - an algorithm for removing inflectional and derivational endings in order to reduce word forms to a common stem algorithm
any methodology for solving a certain kind of problem.
See also: Mathematics

Algorithm
From Wikipedia, the free encyclopedia

Flow chart of an algorithm (Euclid's algorithm) for calculating the greatest common divisor (g.c.d.) of two numbers a and b in locations named A and B. The algorithm proceeds by successive subtractions in two loops: IF the test B ≥ A yields "yes" (or true) (more accurately the number b in location B is greater than or equal to the number a in location A) THEN, the algorithm specifies B ← B − A (meaning the number b − a replaces the old b). Similarly, IF A > B, THEN A ← A − B. The process terminates when (the contents of) B is 0, yielding the g.c.d. in A. (Algorithm derived from Scott 2009:13; symbols and drawing style from Tausworthe 1977).
In mathematics and computer science, an algorithm (i/ˈælɡərɪðəm/) is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and automated reasoning.

More precisely, an algorithm is an effective method expressed as a finite list[1] of well-defined instructions[2] for calculating a function.[3] Starting from an initial state and initial input (perhaps empty),[4] the instructions describe a computation that, when executed, will proceed through a finite [5] number of well-defined successive states, eventually producing "output"[6] and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.[7]

Though al-Khwārizmī's algorism referred to the rules of performing arithmetic using Hindu-Arabic numerals and the systematic solution of linear and quadratic equations, a partial formalization of what would become the modern algorithm began with attempts to solve the Entscheidungsproblem (the "decision problem") posed by David Hilbert in 1928. Subsequent formalizations were framed as attempts to define "effective calculability"[8] or "effective method";[9] those formalizations included the Gödel–Herbrand–Kleene recursive functions of 1930, 1934 and 1935, Alonzo Church's lambda calculus of 1936, Emil Post's "Formulation 1" of 1936, and Alan Turing's Turing machines of 1936–7 and 1939. Giving a formal definition of algorithms, corresponding to the intuitive notion, remains a challenging problem.[10]

Informal definition
For a detailed presentation of the various points of view around the definition of "algorithm" see Algorithm characterizations. For examples of simple addition algorithms specified in the detailed manner described in Algorithm characterizations, see Algorithm examples.
While there is no generally accepted formal definition of "algorithm," an informal definition could be "a set of rules that precisely defines a sequence of operations."[11] For some people, a program is only an algorithm if it stops eventually; for others, a program is only an algorithm if it stops before a given number of calculation steps.[12]

A prototypical example of an algorithm is Euclid's algorithm to determine the maximum common divisor of two integers; an example (there are others) is described by the flow chart above and as an example in a later section.

Boolos & Jeffrey (1974, 1999) offer an informal meaning of the word in the following quotation:

No human being can write fast enough, or long enough, or small enough† ( †"smaller and smaller without limit ...you'd be trying to write on molecules, on atoms, on electrons") to list all members of an enumerably infinite set by writing out their names, one after another, in some notation. But humans can do something equally useful, in the case of certain enumerably infinite sets: They can give explicit instructions for determining the nth member of the set, for arbitrary finite n. Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by a human who is capable of carrying out only very elementary operations on symbols.[13]

The term "enumerably infinite" means "countable using integers perhaps extending to infinity." Thus, Boolos and Jeffrey are saying that an algorithm implies instructions for a process that "creates" output integers from an arbitrary "input" integer or integers that, in theory, can be chosen from 0 to infinity. Thus an algorithm can be an algebraic equation such as y = m + n—two arbitrary "input variables" m and n that produce an output y. But various authors' attempts to define the notion indicate that the word implies much more than this, something on the order of (for the addition example):
Precise instructions (in language understood by "the computer")[14] for a fast, efficient, "good"[15] process that specifies the "moves" of "the computer" (machine or human, equipped with the necessary internally contained information and capabilities)[16] to find, decode, and then process arbitrary input integers/symbols m and n, symbols + and = ... and "effectively"[17] produce, in a "reasonable" time,[18] output-integer y at a specified place and in a specified format.
The concept of algorithm is also used to define the notion of decidability. That notion is central for explaining how formal systems come into being starting from a small set of axioms and rules. In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related with our customary physical dimension. From such uncertainties, that characterize ongoing work, stems the unavailability of a definition of algorithm that suits both concrete (in some sense) and abstract usage of the term.

[edit] Formalization

Algorithms are essential to the way computers process data. Many computer programs contain algorithms that detail the specific instructions a computer should perform (in a specific order) to carry out a specified task, such as calculating employees' paychecks or printing students' report cards. Thus, an algorithm can be considered to be any sequence of operations that can be simulated by a Turing-complete system. Authors who assert this thesis include Minsky (1967), Savage (1987) and Gurevich (2000):

Minsky: "But we will also maintain, with Turing . . . that any procedure which could "naturally" be called effective, can in fact be realized by a (simple) machine. Although this may seem extreme, the arguments . . . in its favor are hard to refute".[19]

Gurevich: "...Turing's informal argument in favor of his thesis justifies a stronger thesis: every algorithm can be simulated by a Turing machine ... according to Savage [1987], an algorithm is a computational process defined by a Turing machine".[20]

Typically, when an algorithm is associated with processing information, data is read from an input source, written to an output device, and/or stored for further processing. Stored data is regarded as part of the internal state of the entity performing the algorithm. In practice, the state is stored in one or more data structures.

For some such computational process, the algorithm must be rigorously defined: specified in the way it applies in all possible circumstances that could arise. That is, any conditional steps must be systematically dealt with, case-by-case; the criteria for each case must be clear (and computable).

Because an algorithm is a precise list of precise steps, the order of computation will always be critical to the functioning of the algorithm. Instructions are usually assumed to be listed explicitly, and are described as starting "from the top" and going "down to the bottom", an idea that is described more formally by flow of control.

So far, this discussion of the formalization of an algorithm has assumed the premises of imperative programming. This is the most common conception, and it attempts to describe a task in discrete, "mechanical" means. Unique to this conception of formalized algorithms is the assignment operation, setting the value of a variable. It derives from the intuition of "memory" as a scratchpad. There is an example below of such an assignment.

For some alternate conceptions of what constitutes an algorithm see functional programming and logic programming.

[edit] Expressing algorithms

Algorithms can be expressed in many kinds of notation, including natural languages, pseudocode, flowcharts, programming languages or control tables (processed by interpreters). Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms. Pseudocode, flowcharts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in natural language statements. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are often used as a way to define or document algorithms.

There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see more at finite state machine, state transition table and control table), as flowcharts (see more at state diagram), or as a form of rudimentary machine code or assembly code called "sets of quadruples" (see more at Turing machine).

Representations of algorithms can be classed into three accepted levels of Turing machine description:[21]
1 High-level description:
"...prose to describe an algorithm, ignoring the implementation details. At this level we do not need to mention how the machine manages its tape or head." 2 Implementation description:
"...prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level we do not give details of states or transition function." 3 Formal description:
Most detailed, "lowest level", gives the Turing machine's "state table". For an example of the simple algorithm "Add m+n" described in all three levels see Algorithm examples.
[edit] Implementation

Most algorithms are intended to be implemented as computer programs. However, algorithms are also implemented by other means, such as in a biological neural network (for example, the human brain implementing arithmetic or an insect looking for food), in an electrical circuit, or in a mechanical device.

[edit] Computer algorithms

Flowchart examples of the canonical Böhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO (IF test=true THEN GOTO step xxx) (a diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks result in complex diagrams (cf Tausworthe 1977:100,114).
In computer systems, an algorithm is basically an instance of logic written in software by software developers to be effective for the intended "target" computer(s), in order for the target machines to produce output from given input (perhaps null).

"Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:
Knuth: ". . .we want good algorithms in some loosely defined aesthetic sense. One criterion . . . is the length of time taken to perform the algorithm . . .. Other criteria are adaptability of the algorithm to computers, its simplicity and elegance, etc"[22] Chaitin: " . . . a program is 'elegant,' by which I mean that it's the smallest possible program for producing the output that it does"[23]
Chaitin prefaces his definition with: "I'll show you can't prove that a program is 'elegant'"—such a proof would solve the Halting problem (ibid).

Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This will be true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is . . . important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".[24]

Unfortunately there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example of using Euclid's algorithm will be shown below.

Computers (and computors), models of computation: A computer (or human "computor"[25]) is a restricted type of machine, a "discrete deterministic mechanical device"[26] that blindly follows its instructions.[27] Melzak's and Lambek's primitive models[28] reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters[29] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[30]

Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability".[31] Minsky's machine proceeds sequentially through its five (or six depending on how one counts) instructions unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution)[32] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[33] Rarely will a programmer have to write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing complete with only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT.[34]

Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example".[35] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectively execute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't then for the algorithm to be effective it must provide a set of rules for extracting a square root.[36]

This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).

But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters".[37] When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" (division) instruction available rather than just subtraction (or worse: just Minsky's "decrement").

Structured programming, canonical structures: Per the Church-Turing thesis any algorithm can be computed by a model known to be Turing complete, and per Minsky's demonstrations Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code" a programmer can write structured programs using these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language".[38] Tausworthe augments the three Böhm-Jacopini canonical structures:[39] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[40] An additional benefit of a structured program will be one that lends itself to proofs of correctness using mathematical induction.[41]

Canonical flowchart symbols[42]: The graphical aide called a flowchart offers a way to describe and document an algorithm (and a computer program of one). Like program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only 4: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm-Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles but only if a single exit occurs from the superstructure. The symbols and their use to build the canonical structures are shown in the diagram.

 

 

EVOLVE LOVE EVOLVE

LOVES SOLVE LOVES

EVOLVE LOVE EVOLVE

 

 

Algorithm - Wikipedia, the free encyclopedia en.wikipedia.org/wiki/Algorithm

In mathematics and computer science, an algorithm is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and ...

 

 

A
=
1
-
9
ALGORITHM
103
49
4
A
=
1
-
10
ALGORITHMS
122
59
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
-
-
ALGORITHMS
-
-
-
-
-
-
-
1
A
1
1
1
-
-
-
-
1
L
12
3
3
-
-
-
-
1
G
7
7
7
-
-
-
-
1
O
15
6
6
-
-
-
-
1
R
18
9
9
-
-
-
-
1
I
9
9
9
-
-
-
-
1
T
20
2
2
-
-
-
-
1
H
8
8
8
-
-
-
-
1
M+S
32
14
5
A
=
1
-
10
ALGORITHMS
122
59
50
-
-
-
-
1+0
-
1+2+2
5+9
5+0
A
=
1
-
1
ALGORITHMS
5
14
5
-
-
-
-
-
-
-
1+4
-
A
=
1
-
1
ALGORITHMS
5
5
5

 

 

-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
-
-
-
6
-
9
-
8
-
1
+
=
24
2+4
=
6
=
6
-
-
-
-
-
15
-
9
-
8
-
19
+
=
51
5+1
=
6
=
6
-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
1
3
7
-
9
-
2
-
4
-
+
=
26
2+6
=
8
=
8
-
-
1
12
7
-
18
-
20
-
13
-
+
=
71
7+1
=
8
=
8
-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
1
12
7
15
18
9
20
8
13
19
+
=
122
1+2+2
=
5
1+0
5
-
-
1
3
7
6
9
9
2
8
4
1
+
=
50
5+0
=
5
1+0
5
-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
2
occurs
x
1
=
2
-
-
-
3
-
-
-
-
-
-
-
-
-
-
3
occurs
x
1
=
3
-
-
-
-
-
-
-
-
-
-
4
-
-
-
4
occurs
x
1
=
4
5
-
-
-
-
-
-
-
-
-
-
-
-
-
5
FIVE
5
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
occurs
x
1
=
6
-
-
-
-
7
-
-
-
-
-
-
-
-
-
7
occurs
x
1
=
7
-
-
-
-
-
-
-
-
-
8
-
-
-
-
8
occurs
x
1
=
8
-
-
-
-
-
-
9
9
-
-
-
-
-
-
9
occurs
x
1
=
9
5
10
A
L
G
O
R
I
T
H
M
S
-
-
27
-
-
10
-
41
-
1+0
-
-
-
-
9
9
-
-
-
-
-
-
2+7
-
-
1+0
-
4+1
5
1
A
L
G
O
R
I
T
H
M
S
-
-
9
-
-
1
-
5
-
-
1
3
7
6
9
9
2
8
4
1
-
-
-
-
-
-
-
-
5
1
A
L
G
O
R
I
T
H
M
S
-
-
9
-
-
1
-
5

 

 

A
=
1
-
10
ALGORITHMS
122
59
5
A
=
1
-
9
ALGORITHM
103
49
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ALGORITHM
-
-
-
A
=
1
-
1
A
1
1
1
L
=
3
-
1
L
12
3
3
G
=
7
-
1
G
7
7
7
O
=
6
-
1
O
15
6
6
R
=
9
-
1
R
18
9
9
I
=
9
-
1
I
9
9
9
T
=
2
-
1
T
20
2
2
H
=
8
-
1
H
8
8
8
M
=
4
-
1
M
13
4
4
-
-
49
-
9
ALGORITHM
103
49
49
-
-
4+9
-
-
-
1+0+3
4+9
4+9
-
-
13
-
9
ALGORITHM
103
13
13
-
-
1+3
-
-
-
-
1+3
1+3
-
-
4
-
9
ALGORITHM
103
4
4

 

 

A
=
1
-
10
ALGORITHMS
122
59
5
A
=
1
-
9
ALGORITHM
103
49
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ALGORITHM
-
-
-
A
=
1
-
1
A
1
1
1
T
=
2
-
1
T
20
2
2
L
=
3
-
1
L
12
3
3
M
=
4
-
1
M
13
4
4
5
-
5
-
-
5
-
-
5
O
=
6
-
1
O
15
6
6
G
=
7
-
1
G
7
7
7
H
=
8
-
1
H
8
8
8
R
=
9
-
1
R
18
9
9
I
=
9
-
1
I
9
9
9
-
-
49
-
9
ALGORITHM
103
49
49
-
-
4+9
-
-
-
1+0+3
4+9
4+9
-
-
13
-
9
ALGORITHM
103
13
13
-
-
1+3
-
-
-
-
1+3
1+3
-
-
4
-
9
ALGORITHM
103
4
4

 

 

A
=
1
-
10
ALGORITHMS
122
59
5
A
=
1
-
9
ALGORITHM
103
49
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ALGORITHM
-
-
-
A
=
1
-
1
A
1
1
1
L
=
3
-
1
L
12
3
3
G
=
7
-
1
G
7
7
7
O
=
6
-
1
O
15
6
6
R
=
9
-
1
R
18
9
9
I
=
9
-
1
I
9
9
9
T
=
2
-
1
T
20
2
2
H
=
8
-
1
H
8
8
8
M
=
4
-
1
M
13
4
4
-
-
49
-
9
ALGORITHM
103
49
49
-
-
4+9
-
-
-
1+0+3
4+9
4+9
-
-
13
-
9
ALGORITHM
103
13
13
-
-
1+3
-
-
-
-
1+3
1+3
-
-
4
-
9
ALGORITHM
103
4
4

 

 

NUMBER

9

THE SEARCH FOR THE SIGMA CODE

Cecil Balmond 1998

Preface to the New Edition

Page 5
Twelve years ago a little boy entered my imagination as he hopped across the centuries and played with numbers. I began to see how the simple architecture of our decimal system could be constructed in secret ways — not a building project this time but an abstract one. On the surface of our arithmetic countless combinations of numbers take part in tedious and exacting calculations but underneath it all there is pattern, governed by a repeating code of integers. The Sigma Code reduces numbers to a single digit and the illusion of the many is seen to be but the reflection of a few. This is not a book on maths: this is a book for anyone who can carry out simple sums in their heads, and who won't be short-changed knowingly.
When Number 9 first came out I received mail from many who played with numbers. They chased patterns; some had special numbers and even mystical systems. I was tempted to write about numerology but resisted. I wanted to write about the intricacy of what the.. numbers actually do and leave the reader to wonder about the larger irrational that seems to hover around such constructions.
If I were writing this book today the numbers would have featured in a wider context of structuring nature's patterns, and also playing the role of animator in algorithms that create unique architectural forms and shapes. I would also include my previous research into other base systems. But this book was a first step which came from a child-like urge, like playing with building blocks, to build out of our numbers — just the simple 1, 2, 3, up to number 9.

 

RESEARCH R E SEARCH ER RESEARCH

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
6
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
-
-
-
-
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
5
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
5
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
5
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
5
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
5
-
-
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
5
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
5
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
5
-
-
8
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
5
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
5
-
-
-
9
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
5
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
6
7
8
9

 

 

logarithm
/ˈlɒɡərɪð(ə)m,-rɪθ-/
noun
noun: logarithm; plural noun: logarithms; noun: log

a quantity representing the power to which a fixed number (the base) must be raised to produce a given number.
"proportional to the logarithm to the base 10 of the concentration"

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
LOGARITHM
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
-
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
-
49
-
9
LOGARITHM
103
49
49
-
1
2
3
4
6
7
8
18
-
-
4+9
-
-
-
1+0+2
4+9
4+9
-
-
-
-
-
-
-
-
1+8
-
-
13
-
9
LOGARITHM
4
13
13
-
1
2
3
4
6
7
8
9
-
-
1+3
-
-
-
-
1+3
1+3
-
-
-
-
-
-
-
-
-
-
-
4
-
9
LOGARITHM
4
4
4
-
1
2
3
4
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LOGARITHM
-
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
5
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
5
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
5
-
7
-
-
A
=
1
4
1
A
1
1
1
-
1
-
3
-
5
-
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
5
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
5
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
5
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
5
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
5
-
-
-
-
-
-
49
-
9
LOGARITHM
103
49
49
-
1
2
3
4
5
6
7
8
18
-
-
4+9
-
-
-
1+0+2
4+9
4+9
-
-
-
-
-
-
-
-
-
1+8
-
-
13
-
9
LOGARITHM
4
13
13
-
1
2
3
4
5
6
7
8
9
-
-
1+3
-
-
-
-
1+3
1+3
-
-
-
-
-
-
-
-
-
-
-
-
4
-
9
LOGARITHM
4
4
4
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LOGARITHM
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
5
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
5
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
5
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
5
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
5
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
5
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
5
-
-
8
-
I
=
9
6
1
I
9
9
9
-
-
-
-
-
5
-
-
-
9
R
=
9
5
1
R
18
9
9
-
-
-
-
-
5
-
-
-
9
-
-
49
-
9
LOGARITHM
103
49
49
-
1
2
3
4
5
6
7
8
18
-
-
4+9
-
-
-
1+0+2
4+9
4+9
-
-
-
-
-
-
-
-
-
1+8
-
-
13
-
9
LOGARITHM
4
13
13
-
1
2
3
4
5
6
7
8
9
-
-
1+3
-
-
-
-
1+3
1+3
-
-
-
-
-
-
-
-
-
-
-
-
4
-
9
LOGARITHM
4
4
4
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
LOGARITHM
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
-
-
49
-
9
LOGARITHM
103
49
49
-
1
2
3
4
6
7
8
18
-
-
4+9
-
-
-
1+0+2
4+9
4+9
-
-
-
-
-
-
-
-
1+8
-
-
13
-
9
LOGARITHM
4
13
13
-
1
2
3
4
6
7
8
9
-
-
1+3
-
-
-
-
1+3
1+3
-
-
-
-
-
-
-
-
-
-
-
4
-
9
LOGARITHM
4
4
4
-
1
2
3
4
6
7
8
9

 

LOGARITHM

 

LOGARITHMS

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LOGARITHMS
-
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
5
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
5
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
5
-
7
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
5
-
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
5
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
5
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
5
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
5
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
5
-
-
-
-
S
=
1
10
1
S
19
10
1
-
1
-
-
-
5
-
-
-
-
-
-
41
-
10
LOGARITHMS
122
50
41
-
1
2
3
4
5
6
7
8
18
-
-
4+1
-
1+0
-
1+2+2
5+0
5+0
-
-
-
-
-
-
-
-
-
1+8
-
-
5
-
9
LOGARITHMS
5
5
5
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
LOGARITHMS
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
-
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
S
=
1
10
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
-
41
-
10
LOGARITHMS
122
50
41
-
1
2
3
4
6
7
8
18
-
-
4+1
-
1+0
-
1+2+2
5+0
5+0
-
-
-
-
-
-
-
-
1+8
-
-
5
-
9
LOGARITHMS
5
5
5
-
1
2
3
4
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LOGARITHMS
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
5
-
-
-
-
S
=
1
10
1
S
19
10
1
-
1
-
-
-
5
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
5
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
5
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
5
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
5
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
5
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
5
-
-
8
-
I
=
9
6
1
I
9
9
9
-
-
-
-
-
5
-
-
-
9
R
=
9
5
1
R
18
9
9
-
-
-
-
-
5
-
-
-
9
-
-
41
-
10
LOGARITHMS
122
50
41
-
1
2
3
4
5
6
7
8
18
-
-
4+1
-
1+0
-
1+2+2
5+0
5+0
-
-
-
-
-
-
-
-
-
1+8
-
-
5
-
9
LOGARITHMS
5
5
5
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
LOGARITHMS
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
4
1
A
1
1
1
-
1
-
-
-
-
-
-
-
S
=
1
10
1
S
19
10
1
-
1
-
-
-
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
L
=
3
1
1
L
12
3
3
-
-
-
3
-
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
O
=
6
2
1
O
15
6
6
-
-
-
-
-
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
-
-
41
-
10
LOGARITHMS
122
50
41
-
1
2
3
4
6
7
8
18
-
-
4+1
-
1+0
-
1+2+2
5+0
5+0
-
-
-
-
-
-
-
-
1+8
-
-
5
-
9
LOGARITHMS
5
5
5
-
1
2
3
4
6
7
8
9

 

 

Math Forum: Ask Dr. Math FAQ: About e

mathforum.org/dr.math/faq/faq.e.html

e = 2.71828..., the Base of Natural Logarithms. e is a real number constant that appears in some kinds of mathematics problems. Examples of such problems are those ...

_____________________________________________


What is e? Who first used e? How do you find it? How many digits does it have?

e = 2.71828..., the Base of Natural Logarithms

e is a real number constant that appears in some kinds of mathematics problems. Examples of such problems are those involving growth or decay (including compound interest), the statistical "bell curve," the shape of a hanging cable (or the Gateway Arch in St. Louis), some problems of probability, some counting problems, and even the study of the distribution of prime numbers. It appears in Stirling's Formula for approximating factorials. It also shows up in calculus quite often, wherever you are dealing with either logarithmic or exponential functions. There is also a connection between e and complex numbers, via Euler's Equation.

e is usually defined by the following equation:

e = limn->infinity (1 + 1/n)n.

Its value is approximately 2.718281828459045... and has been calculated to 869,894,101 decimal places by Sebastian Wedeniwski (you'll find the first 50 digits in a Table of constants with 50 decimal places, from the Numbers, constants and computation site, by Xavier Gourdon and Pascal Sebah).

The number e was first studied by the Swiss mathematician Leonhard Euler in the 1720s, although its existence was more or less implied in the work of John Napier, the inventor of logarithms, in 1614. Euler was also the first to use the letter e for it in 1727 (the fact that it is the first letter of his surname is coincidental). As a result, sometimes e is called the Euler Number, the Eulerian Number, or Napier's Constant (but not Euler's Constant).

An effective way to calculate the value of e is not to use the defining equation above, but to use the following infinite sum:

e = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + ...

If you need K decimal places, compute each term to K+3 decimal places and add them up. You can stop adding after the term 1/n! where n! > 10K+3, because, to K+3 decimal places, the rest of the terms are all zero. Even though there are infinitely many of them, they will not change the decimal places you have already calculated. Now the last decimal place or two of the resulting sum may be off due to truncation or rounding of each term, but the first K places should be correct. That is why the computation uses extra decimal places.

As an example, here is the computation of e to 22 decimal places:
1/0! = 1/1 = 1.0000000000000000000000000
1/1! = 1/1 = 1.0000000000000000000000000
1/2! = 1/2 = 0.5000000000000000000000000
1/3! = 1/6 = 0.1666666666666666666666667
1/4! = 1/24 = 0.0416666666666666666666667
1/5! = 1/120 = 0.0083333333333333333333333
1/6! = 1/720 = 0.0013888888888888888888889
1/7! = 1/5040 = 0.0001984126984126984126984
1/8! = 1/40320 = 0.0000248015873015873015873
1/9! = 1/362880 = 0.0000027557319223985890653
1/10! = 1/3628800 = 0.0000002755731922398589065
1/11! = 0.0000000250521083854417188
1/12! = 0.0000000020876756987868099
1/13! = 0.0000000001605904383682161
1/14! = 0.0000000000114707455977297
1/15! = 0.0000000000007647163731820
1/16! = 0.0000000000000477947733239
1/17! = 0.0000000000000028114572543
1/18! = 0.0000000000000001561920697
1/19! = 0.0000000000000000082206352
1/20! = 0.0000000000000000004110318
1/21! = 0.0000000000000000000195729
1/22! = 0.0000000000000000000008897
1/23! = 0.0000000000000000000000387
1/24! = 0.0000000000000000000000016
1/25! = 0.0000000000000000000000001
-----------------------------
2.7182818284590452353602875

Then to 22 decimal places, e = 2.7182818284590452353603, which is correct. (Actually,it's correct to 25 places, but that was luck!).
There have been recent discoveries of even more efficient ways of computing e, one of which was used for setting the record mentioned above.

It is a fact (proved by Euler) that e is an irrational number, so its decimal expansion never terminates, nor is it eventually periodic. Thus no matter how many digits in the expansion of e you know, the only way to predict the next one is to compute e using the method above using more accuracy.

It is also true that e is a transcendental number (a fact first proved in 1873 by the French mathematician Charles Hermite), which means that e is not the root of any polynomial with rational number coefficients. These are properties that e shares with pi. The Dr. Math archives contain one proof of The Irrationality of e, and on the Web is another by Kevin Brown.

e is also the base of natural logarithms. The natural logarithm function ln(x) is defined that way: ln(x) = loge(x). This is "natural" for several reasons. One is the following limit:

 

ln(x) = limk->0 (xk-1)/k.

Another example from calculus is that if y = ln(x) + c, for c constant, then dy/dx = 1/x, and these are the only functions for which this is true. Another is that the curve y = ln(x) has a tangent at (1,0) with slope 1, and among all logarithmic functions, it is the only one that does.

Note: The term Euler's Constant is usually reserved for another number also first studied by Euler, 0.5772156649... = limn->infinity [1/1 + 1/2 + 1/3 + ... + 1/n - ln(n)]. [Return to text.]

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
ALGEBRA
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
B
=
2
5
1
B
20
2
2
-
-
2
-
-
-
-
-
-
-
R
=
9
6
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
A
=
1
7
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
-
-
28
-
7
ALGEBRA
46
28
28
-
2
2
3
4
5
6
7
8
9
-
-
2+8
-
-
-
4+6
2+8
2+8
-
-
-
-
-
-
-
-
-
-
-
-
10
-
7
ALGEBRA
10
10
10
-
2
2
3
4
5
6
7
8
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
7
ALGEBRA
1
1
1
-
2
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
ALGEBRA
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
4
-
6
-
8
-
L
=
3
2
1
L
12
3
3
-
-
-
3
4
-
6
-
8
-
G
=
7
3
1
G
7
7
7
-
-
-
-
4
-
6
7
8
-
E
=
5
4
1
E
5
5
5
-
-
-
-
4
5
6
-
8
-
B
=
2
5
1
B
20
2
2
-
-
2
-
4
-
6
-
8
-
R
=
9
6
1
R
18
9
9
-
-
-
-
4
-
6
-
8
9
A
=
1
7
1
A
1
1
1
-
1
-
-
4
-
6
-
8
-
-
-
28
-
7
ALGEBRA
46
28
28
-
2
2
3
4
5
6
7
8
9
-
-
2+8
-
-
-
4+6
2+8
2+8
-
-
-
-
-
-
-
-
-
-
-
-
10
-
7
ALGEBRA
10
10
10
-
2
2
3
4
5
6
7
8
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
7
ALGEBRA
1
1
1
-
2
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
ALGEBRA
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
4
-
6
-
8
-
A
=
1
7
1
A
1
1
1
-
1
-
-
4
-
6
-
8
-
B
=
2
5
1
B
20
2
2
-
-
2
-
4
-
6
-
8
-
L
=
3
2
1
L
12
3
3
-
-
-
3
4
-
6
-
8
-
E
=
5
4
1
E
5
5
5
-
-
-
-
4
5
6
-
8
-
G
=
7
3
1
G
7
7
7
-
-
-
-
4
-
6
7
8
-
R
=
9
6
1
R
18
9
9
-
-
-
-
4
-
6
-
8
9
-
-
28
-
7
ALGEBRA
46
28
28
-
2
2
3
4
5
6
7
8
9
-
-
2+8
-
-
-
4+6
2+8
2+8
-
-
-
-
-
-
-
-
-
-
-
-
10
-
7
ALGEBRA
10
10
10
-
2
2
3
4
5
6
7
8
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
7
ALGEBRA
1
1
1
-
2
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
5
7
9
-
-
-
-
-
ALGEBRA
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
A
=
1
7
1
A
1
1
1
-
1
-
-
-
-
-
B
=
2
5
1
B
20
2
2
-
-
2
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
5
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
7
-
R
=
9
6
1
R
18
9
9
-
-
-
-
-
-
9
-
-
28
-
7
ALGEBRA
46
28
28
-
2
2
3
5
7
9
-
-
2+8
-
-
-
4+6
2+8
2+8
-
-
-
-
-
-
-
-
-
10
-
7
ALGEBRA
10
10
10
-
2
2
3
5
7
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
1
-
7
ALGEBRA
1
1
1
-
2
2
3
5
7
9

 

 

-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
-
-
-
3
-
-
-
-
-
-
-
3
occurs
x
1
=
3
4
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
5
-
-
-
-
-
5
occurs
x
1
=
5
6
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
7
-
-
-
-
-
-
7
occurs
x
1
=
7
8
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
9
-
-
-
9
occurs
x
1
=
9
18
7
A
L
G
E
B
R
A
-
-
27
-
-
7
-
28
1+8
-
-
-
-
-
-
9
-
-
-
2+7
-
-
-
-
2+8
9
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
10
-
-
1
3
7
5
2
9
1
-
-
-
-
-
-
-
1+0
9
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
1

 

 

7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
-
-
3
-
-
-
-
-
-
-
3
occurs
x
1
=
3
-
-
-
-
5
-
-
-
-
-
5
occurs
x
1
=
5
-
-
-
7
-
-
-
-
-
-
7
occurs
x
1
=
7
-
-
-
-
-
-
9
-
-
-
9
occurs
x
1
=
9
7
A
L
G
E
B
R
A
-
-
27
-
-
7
-
28
-
-
-
-
-
-
9
-
-
-
2+7
-
-
-
-
2+8
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
10
-
1
3
7
5
2
9
1
-
-
-
-
-
-
-
1+0
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
1

 

 


So, our Decimal System lets us write numbers as large or as small as we want, using the decimal point. Digits can be placed to the left or right of a decimal point, to show values greater than one or less than one. The decimal point is the most important part of a Decimal Number.
Decimals - Math is Fun

https://www.mathsisfun.com/decimals.html

 

T
=
2
-
3
THE
33
15
6
D
=
4
-
7
DECIMAL
47
29
2
S
=
1
-
6
SYSTEM
101
20
2
-
-
7
-
16
First Total
181
64
10
-
-
-
-
1+6
Add to Reduce
1+8+1
6+4
1+0
-
-
7
-
7
Second Total
10
10
1
-
-
-
-
-
Reduce to Produce
1+0
1+0
-
-
-
7
-
7
Essence of Number
1
1
1

 


Decimal - Wikipedia

https://en.wikipedia.org/wiki/Decimal

A decimal number, or just decimal, refers to any number written in decimal notation, although it is more commonly used to refer to numbers that have a fractional part separated from the integer part with a decimal separator (e.g. 11.25).

The decimal numeral system (also called base-ten and occasionally called denary) has ten as its base, which, in decimal, is written 10, as is the base in every positional numeral system. It is the numerical base most widely used by modern civilizations.[1]
Decimal notation often refers to a base-1000 positional notation such as the Hindu-Arabic numeral system; [2] however, it can also be used more generally to refer to non-positional systems such as Roman or Chinese numerals which are also based on powers of ten.
A decimal number, or just decimal, refers to any number written in decimal notation, although it is more commonly used to refer to numbers that have a fractional part separated from the integer part with a decimal separator (e.g. 11.25).
A decimal may be a terminating decimal, which has a finite fractional part (e.g. 15.600); a repeating decimal, which has an infinite (non-terminating) fractional part made up of a repeating sequence of digits (e.g. 5.123144[3]); or an infinite decimal, which has a fractional part that neither terminates nor has an infinitely repeating pattern (e.g. 3.14159265...). Decimal fractions have terminating decimal representations and other fractions have repeating decimal representations, whereas irrational numbers have infinite non-repeating decimal representations

Decimal notation is the writing of numbers in a base-ten numeral system. Examples are Brahmi numerals, Greek numerals, Hebrew numerals, Roman numerals, and Chinese numerals, as well as the Hindu-Arabic numerals used by speakers of many European languages. Roman numerals have symbols for the decimal powers (1, 10, 100, 1000) and secondary symbols for half these values (5, 50, 500). Brahmi numerals have symbols for the nine numbers 1–9, the nine decades 10–90, plus a symbol for 100 and another for 1000. Chinese numerals have symbols for 1–9, and additional symbols for powers of ten, which in modern usage reach 1072.
However, when people who use Hindu-Arabic numerals speak of decimal notation, they often mean not just decimal numeration, as above, but also decimal fractions, all conveyed as part of a positional system. Positional decimal systems include a zero and use symbols (called digits) for the ten values (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) to represent any number, no matter how large or how small. These digits are often used with a decimal separator which indicates the start of a fractional part, and with a symbol such as the plus sign + (for positive) or minus sign - (for negative) adjacent to the numeral to indicate whether it is greater or less than zero, respectively.
Positional notation uses positions for each power of ten: units, tens, hundreds, thousands, etc. The position of each digit within a number denotes the multiplier (power of ten) multiplied with that digit—each position has a value ten times that of the position to its right. There were at least two presumably independent sources of positional decimal systems in ancient civilization: the Chinese counting rod system and the Hindu-Arabic numeral system (the latter descended from Brahmi numerals).

Ten fingers on two hands, the possible starting point of the decimal counting.
Ten is the number which is the count of fingers and thumbs on both hands (or toes on the feet). The English word digit as well as its translation in many languages is also the anatomical term for fingers and toes. In English, decimal (decimus < Lat.) means tenth, decimate means reduce by a tenth, and denary (denarius < Lat.) means the unit of ten.

The symbols for the digits in common use around the globe today are called Arabic numerals by Europeans and Indian numerals by Arabs, the two groups' terms both referring to the culture from which they learned the system. However, the symbols used in different areas are not identical; for instance, Western Arabic numerals (from which the European numerals are derived) differ from the forms used by other Arab cultures.

 

 

-
-
-
-
-
GEOMETRY
-
-
-
-
1
2
3
4
5
6
7
8
9
G
=
7
-
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
-
-
45
-
8
GEOMETRY
108
45
45
-
1
2
3
4
10
6
14
8
9
-
-
4+5
-
-
-
1+0+8
4+5
4+5
-
-
-
-
-
1+0
-
1+4
-
-
-
-
9
-
8
GEOMETRY
9
9
9
-
1
2
3
4
1
6
5
8
9

 

 

-
-
-
-
-
GEOMETRY
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
G
=
7
-
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
-
-
45
-
8
GEOMETRY
108
45
45
-
1
2
3
4
10
6
14
8
9
-
-
4+5
-
-
-
1+0+8
4+5
4+5
-
-
-
-
-
1+0
-
1+4
-
-
-
-
9
-
8
GEOMETRY
9
9
9
-
1
2
3
4
1
6
5
8
9

 

 

-
-
-
-
-
GEOMETRY
-
-
-
-
2
4
5
6
7
9
T
=
2
-
1
T
20
2
2
-
2
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
4
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
5
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
5
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
6
-
-
G
=
7
-
1
G
7
7
7
-
-
-
-
-
7
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
7
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
9
-
-
45
-
8
GEOMETRY
108
45
45
-
2
4
10
6
14
9
-
-
4+5
-
-
-
1+0+8
4+5
4+5
-
-
-
1+0
-
1+4
-
-
-
9
-
8
GEOMETRY
9
9
9
-
2
4
1
6
5
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
PROBLEMS
-
-
-
-
-
-
-
-
-
-
-
-
-
P
=
7
1
1
P
16
7
7
-
-
-
-
-
-
-
7
-
-
R
=
9
2
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
O
=
6
3
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
B
=
2
4
1
B
2
2
2
-
-
2
-
-
-
-
-
-
-
L
=
3
5
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
E
=
5
6
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
M
=
4
7
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
S
=
1
8
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
-
-
37
-
8
PROBLEMS
100
46
37
-
1
2
3
4
5
6
7
8
9
-
-
3+7
-
-
-
1+0+0
4+6
3+7
-
-
-
-
-
-
-
-
-
-
-
-
10
-
8
PROBLEMS
10
10
10
-
1
2
3
4
5
6
7
8
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
8
PROBLEMS
1
1
1
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
PROBLEMS
-
-
-
-
-
-
-
-
-
-
-
-
-
P
=
7
1
1
P
16
7
7
-
-
-
-
-
-
-
7
8
-
R
=
9
2
1
R
18
9
9
-
-
-
-
-
-
-
-
8
9
O
=
6
3
1
O
15
6
6
-
-
-
-
-
-
6
-
8
-
B
=
2
4
1
B
2
2
2
-
-
2
-
-
-
-
-
8
-
L
=
3
5
1
L
12
3
3
-
-
-
3
-
-
-
-
8
-
E
=
5
6
1
E
5
5
5
-
-
-
-
-
5
-
-
8
-
M
=
4
7
1
M
13
4
4
-
-
-
-
4
-
-
-
8
-
S
=
1
8
1
S
19
10
1
-
1
-
-
-
-
-
-
8
-
-
-
37
-
8
PROBLEMS
100
46
37
-
1
2
3
4
5
6
7
8
9
-
-
3+7
-
-
-
1+0+0
4+6
3+7
-
-
-
-
-
-
-
-
-
-
-
-
10
-
8
PROBLEMS
10
10
10
-
1
2
3
4
5
6
7
8
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
8
PROBLEMS
1
1
1
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
PROBLEMS
-
-
-
-
-
-
-
-
-
-
-
-
-
S
=
1
8
1
S
19
10
1
-
1
-
-
-
-
-
-
8
-
B
=
2
4
1
B
2
2
2
-
-
2
-
-
-
-
-
8
-
L
=
3
5
1
L
12
3
3
-
-
-
3
-
-
-
-
8
-
M
=
4
7
1
M
13
4
4
-
-
-
-
4
-
-
-
8
-
E
=
5
6
1
E
5
5
5
-
-
-
-
-
5
-
-
8
-
O
=
6
3
1
O
15
6
6
-
-
-
-
-
-
6
-
8
-
P
=
7
1
1
P
16
7
7
-
-
-
-
-
-
-
7
8
-
R
=
9
2
1
R
18
9
9
-
-
-
-
-
-
-
-
8
9
-
-
37
-
8
PROBLEMS
100
46
37
-
1
2
3
4
5
6
7
8
9
-
-
3+7
-
-
-
1+0+0
4+6
3+7
-
-
-
-
-
-
-
-
-
-
-
-
10
-
8
PROBLEMS
10
10
10
-
1
2
3
4
5
6
7
8
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
8
PROBLEMS
1
1
1
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
9
-
-
-
-
-
PROBLEMS
-
-
-
-
-
-
-
-
-
-
-
-
S
=
1
8
1
S
19
10
1
-
1
-
-
-
-
-
-
-
B
=
2
4
1
B
2
2
2
-
-
2
-
-
-
-
-
-
L
=
3
5
1
L
12
3
3
-
-
-
3
-
-
-
-
-
M
=
4
7
1
M
13
4
4
-
-
-
-
4
-
-
-
-
E
=
5
6
1
E
5
5
5
-
-
-
-
-
5
-
-
-
O
=
6
3
1
O
15
6
6
-
-
-
-
-
-
6
-
-
P
=
7
1
1
P
16
7
7
-
-
-
-
-
-
-
7
-
R
=
9
2
1
R
18
9
9
-
-
-
-
-
-
-
-
9
-
-
37
-
8
PROBLEMS
100
46
37
-
1
2
3
4
5
6
7
9
-
-
3+7
-
-
-
1+0+0
4+6
3+7
-
-
-
-
-
-
-
-
-
-
-
10
-
8
PROBLEMS
10
10
10
-
1
2
3
4
5
6
7
9
-
-
1+0
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
1
-
8
PROBLEMS
1
1
1
-
1
2
3
4
5
6
7
9

 

 

T
=
2
-
5
THREE
56
29
2
S
=
1
-
3
SIX
52
25
7
N
=
5
-
4
NINE
42
24
6
-
-
8
-
12
First Total
150
78
15
-
-
-
-
1+2
Add to Reduce
1+5+0
7+8
1+5
-
-
8
-
3
Second Total
6
15
6
-
-
-
-
-
Reduce to Produce
-
1+5
-
-
-
8
-
3
Essence of Number
6
6
6

 

 

-
-
-
-
CIRCLE
-
-
-
-
-
-
1
C
3
3
3
-
-
-
1
I
9
9
9
-
-
-
1
R
18
9
9
-
-
-
1
C
3
3
3
-
-
-
1
L
12
3
3
-
-
-
1
E
5
5
5
C
=
3
6
CIRCLE
50
32
32
-
-
-
-
-
5+0
3+2
3+2
C
=
3
6
CIRCLE
5
5
5

 

 

-
-
-
-
CIRCLE
-
-
-
-
-
-
5
CIRCL
45
27
9
-
-
-
1
E
5
5
5
C
=
3
6
CIRCLE
50
32
32
-
-
-
-
-
5+0
3+2
3+2
C
=
3
6
CIRCLE
5
5
5

 

 

T
=
2
-
3
THE
33
15
6
C
=
3
-
6
CIRCLE
50
32
5
I
=
9
-
2
IS
28
10
1
P
=
7
-
7
PERFECT
73
37
1
I
=
9
-
2
IS
28
10
1
P
=
7
-
7
PERFECT
73
37
1
I
=
9
-
2
IS
28
10
1
T
=
2
-
3
THE
33
15
6
C
=
3
-
6
CIRCLE
50
32
5
-
-
51
-
38
First Total
396
198
27
-
-
5+1
-
3+8
Add to Reduce
3+9+6
1+9+8
2+7
-
-
6
-
11
Second Total
18
18
9
-
-
-
-
1+1
Reduce to Deduce
1+8
1+8
-
-
-
6
-
2
Essence of Number
9
9
9

 

 

The circle is a universal symbol with extensive meaning. It represents the notions of totality, wholeness, original perfection, the Self, the infinite, eternity, timelessness, all cyclic movement, God ('God is a circle whose centre is everywhere and whose circumference is nowhere' (Hermes Trismegistus).

 

3
THE
33
15
6
6
CIRCLE
50
32
5
2
OF
21
12
3
3
THE
33
15
6
5
CYCLE
48
21
3
19
First Total
185
95
23
1+9
Add to Reduce
1+8+5
9+5
2+3
10
Second Total
14
14
5
1+0
Reduce to Deduce
1+4
1+4
-
1
Essence of Number
5
5
5

 

The Chronology of Stone Circles:

9,000 BC

Gobekli Tepe, Turkey. The oldest known megalithic temple/circle in the world.

3,200 BC Stonehenge I, Barford Henge, Arminghall Henge (1)
3,100 BC Ballynoe, Carles (1)
2,950 BC Stennes (1)
2,600 BC Stonehenge II, Avebury (1)

14 more rows

www.ancient-wisdom.com/stonecircles.htm

 

 

45
-
F
=
6
-
9
FORTYFIVE
126
54
9
54
-
F
=
6
-
9
FIFTY FOUR
126
54
9
63
-
S
=
1
-
10
SIXTYTHREE
153
54
9
81
-
E
=
5
-
9
EIGHTYONE
108
54
9
243
-
-
-
18
-
37
-
513
216
36
2+4+3
-
-
-
4+6
-
3+7
-
5+1+3
5+1+2
3+6
9
-
-
-
10
-
12
-
9
9
9
-
-
-
-
1+0
-
1+2
-
-
-
-
9
-
-
-
1
-
3
-
9
9
9

 

 

9
FORTY FIVE
126
54
9
9
FIFTY FOUR
126
54
9
18
-
252
108
18
1+8
-
2+5+2
1+0+8
1+8
9
-
9
9
9

 

 

81
-
9
EIGHTY ONE
108
54
9
54
-
9
FIFTY FOUR
126
54
9
135
-
18
-
234
108
18
1+3+5
-
1+8
-
2+3+4
1+0+8
1+8
9
-
9
-
9
9
9

 

 

9
NINETY SIX
139
58
4
9
SIXTY NINE
139
58
4

 

 

4
NINE
42
24
6
10
NINETY NINE
129
57
3
14
Add to reduce
171
81
9
1+4
Reduce to dedeuce
1+7+1
8+1
-
5
Essence of number
9
9
9

 

 

14
NINE NINETY NINE
171
81
9

 

 

 

14
NINE NINE NINE
171
81
9
4
NINE
42
24
6
4
NINE
42
24
6
4
NINE
42
24
6
12
NINE NINE NINE
126
72
18
1+2
-
1+2+6
7+2
1+8
3
NINE NINE NINE
9
9
9

 

 

14
NINENINENINE
171
81
9
2
NI
23
14
5
1
N
14
5
5
1
E
5
5
5
2
NI
23
14
5
1
N
14
5
5
1
E
5
5
5
1
N
14
14
5
2
IN
23
14
5
1
E
5
5
5
12
NINENINENINE
126
72
45
1+2
-
1+2+6
7+2
4+5
3
NINENINENINE
9
9
9

 

 

14
NINENINENINE
171
81
9
1
N
14
5
5
1
I
9
9
9
1
N
14
5
5
1
E
5
5
5
1
N
14
5
5
1
I
9
9
9
1
N
14
5
5
1
E
5
5
5
1
N
14
5
5
1
I
9
9
9
2
N
14
5
5
1
E
5
5
5
12
NINENINENINE
126
72
45
1+2
-
1+2+6
7+2
4+5
3
NINENINENINE
9
9
9

 

 

14
NINENINENINE
171
81
9
2
NI
23
14
5
1
N
14
5
5
1
E
5
5
5
2
NI
23
14
5
1
N
14
5
5
1
E
5
5
5
3
N
14
5
5
2
NI
23
14
5
1
E
5
5
5
12
NINENINENINE
126
72
45
1+2
-
1+2+6
7+2
4+5
3
NINENINENINE
9
9
9

 

From: Dave Denison
Sent: Wednesday, February 1, 2017 11:01 PM
To:
Subject: FIRST OF FEBRUARY 2017

I SAY, IS THIS THE OTHER SIDE OF THE ROAD?
NO, ITS OVER THERE.
I’VE JUST BEEN OVER THERE, AND THEY SAID IT WAS OVER HERE.

 

MIND BORN SONS, THOSE PATENT PATIENT PATENTED PATTERN MAKERS.
MIND=4 BORN=4 SONS=4 THOSE=4 PATENT=4 PATIENT=4 PATENTED=4 PATTERN=4 MAKERS=4

Usage Statistics for 973-eht-namuh-973.com
Summary by Month
Generated 01-Feb-2017 13:18 GMT

 

Daily Statistics for January 2017
Day Hits Files Pages Visits Sites KBytes
31 85406 3.01% 60606 2.82% 20395 4.74% 4013 3.82% 3624 6.15% 4444095 2.78%

KBytes 4444095

THANK YOU FOR YOUR TREASURED MEASURE = 444

 

fourforfour
Posts: 1
Joined: 21 Feb 2017 14:03
Contact:
Contact fourforfour
Followed by 444

Post by fourforfour » 21 Feb 2017 14:49

"Hello, I have never posted on here and have just made this account, however I have been visiting this site for a couple of years now. Forgive me, this may not belong on here but I'm not sure that there's any group of people better suited to give me insight than all of you.
Over the past year, I have found myself being followed by a number, 444. This first started happening a year ago. My friends and I decided to write notes and then burn them together on new years. I wrote two notes, one about my past, and one about my future. In the future note, I asked for some kind of sign so I would know my notes and messages had been read and seen by, well, whatever higher power there is. I'll refer to it as the universe I suppose. That's when I started being followed by 444. I would wake up at 4:44 am, and my phone would be on 44%. This happened day after day. It would be 4:44 pm, and my phone would be on 44%, day after day after day. I then stumbled upon a song on YouTube, it was titled something along the lines of New Years Eve. It had 444 views and 44 likes. I see it everywhere. License plates, the numbers of likes and comments on social media apps and sites, taxi cabs, commercials, songs, the hospital, anywhere it could show up it shows up. Sometimes I can connect it to things going on in my life depending on where and what I see it on, and every time I can connect it in some way it foreshadows the future. Other times it's just there, and I can't connect it to anything. I've googled it and researched it all I can, but it hasn't helped me much. I've tried to find possible meanings behind it on here as well, but so far I haven't found anything worth noting.
I was wondering if any of you have had a similar experience, or if any of you have found/can find something on here about the number. I'd just like to understand more about this number, and what it means. Hopefully someone on here can help me."

21 x 4 = 84

 

MIND BORN SONS, THOSE PATENT PATIENT PATENTED PATTERN MAKERS

MIND=4 BORN=4 SONS=4 THOSE=4 PATENT=4 PATIENT=4 PATENTED=4 PATTERN=4 MAKERS=4

THANK YOU FOR YOUR TREASURED MEASURE = 444

 

T
=
2
-
5
THANK
54
18
9
Y
=
7
-
3
YOU
61
16
7
F
=
6
-
3
FOR
57
21
3
Y
=
2
-
4
YOUR
79
25
7
T
=
2
-
9
TREASURED
111
39
3
M
=
4
-
7
MEASURE
82
28
1
-
-
28
4
43
First Total
444
147
30
-
-
2+8
-
4+3
Add to Reduce
4+4+4
1+4+7
3+0
Q
-
10
-
7
Second Total
12
12
3
-
-
1+0
-
-
Reduce to Produce
1+2
1+2
-
Q
-
1
-
7
Essence of Number
3
3
3

 

 

-
FOURTEEN
-
-
-
1
F
6
6
6
2
OU
36
9
9
1
R
18
18
9
4
TEEN
44
17
8
8
FOURTEEN
104
50
32
-
-
1+0+4
5+0
3+2
8
FOURTEEN
5
5
5

 

 

-
-
-
-
-
FOURTEEN
-
-
-
-
-
-
-
-
14 1+4 = 5
-
-
-
-
-
-
-
-
FOURTEEN
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
FOURTEEN
-
-
-
F
=
6
-
4
FOUR
60
24
6
T
=
2
-
4
TEEN
44
17
8
-
-
8
-
8
FOURTEEN
104
41
14
-
-
-
-
-
-
1+0+4
4+1
1+4
-
-
8
-
8
FOURTEEN
5
5
5

 

 

-
8
F
O
U
R
T
E
E
N
-
-
-
-
-
-
-
--
-
-
-
-
-
6
-
-
-
-
-
5
+
=
11
1+1
=
2
-
2
-
2
-
-
-
15
-
-
-
-
-
14
+
=
29
2+9
=
11
1+1
2
-
2
-
8
F
O
U
R
T
E
E
N
-
-
-
-
-
-
-
-
-
-
-
-
6
-
3
9
2
5
5
-
+
=
30
3+0
=
3
-
3
-
3
-
-
6
-
21
18
20
5
5
-
+
=
75
7+5
=
12
1+2
3
-
3
-
8
F
O
U
R
T
E
E
N
-
-
-
-
-
-
-
-
-
-
-
-
6
15
21
18
20
5
5
14
+
=
104
1+0+4
=
5
=
5
-
5
-
-
6
6
3
9
2
5
5
5
+
=
41
4+1
=
5
=
5
-
5
-
8
F
O
U
R
T
E
E
N
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
-
-
-
1
ONE
1
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
-
3
-
-
-
-
-
-
-
3
occurs
x
1
=
3
=
3
4
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
-
-
-
-
5
5
5
-
-
5
occurs
x
3
=
15
1+5
6
-
-
6
6
-
-
-
-
-
-
-
-
6
occurs
x
2
=
12
1+2
3
7
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
9
occurs
x
1
=
9
-
9
20
8
F
O
U
R
T
E
E
N
-
-
25
-
-
8
-
41
-
23
2+0
-
-
-
-
-
-
5
5
5
-
-
2+5
-
--
-
-
4+1
-
2+3
2
8
F
O
U
R
T
E
E
N
-
-
7
-
-
8
-
5
-
5
-
-
6
6
3
9
2
5
5
5
-
-
-
-
-
--
--
-
-
-
2
8
F
O
U
R
T
E
E
N
-
-
7
-
-
8
-
5
-
5

 

 

FOUR FOUR FOUR = 6-6-6
SIX SIX SIX = 7-7-7
SEVEN SEVEN SEVEN = 2-2-2
TWO TWO TWO = 4-4-4
FOUR FOUR FOUR = 6-6-6

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
FOUR FOUR FOUR
-
-
-
-
-
-
-
-
-
-
-
-
-
F
=
6
1
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
3
2
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
U
=
3
3
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
R
=
9
4
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
F
=
6
5
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
3
6
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
U
=
7
7
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
R
=
9
8
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
F
=
6
9
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
3
10
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
U
=
7
11
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
R
=
9
12
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
-
-
72
-
10
FOUR FOUR FOUR
153
72
72
-
1
2
9
4
5
36
7
8
18
-
-
7+2
-
1+0
-
1+5+3
7+2
7+2
-
-
-
-
-
-
3+6
-
-
1+8
-
-
9
-
1
FOUR FOUR FOUR
9
9
9
-
1
2
9
4
5
9
7
8
9

 

 

-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
--
-
-
-
-
-
-
-
6
-
-
-
-
6
-
-
-
-
6
-
-
+
=
18
1+8
=
9
=
9
=
9
-
-
-
15
-
-
-
-
15
-
-
-
-
15
-
-
+
=
54
5+4
=
9
=
9
=
9
-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
--
-
-
-
-
-
-
6
-
3
9
-
6
-
3
9
-
6
-
3
9
+
=
54
5+4
=
9
=
9
=
9
-
-`
6
-
21
18
-
6
-
21
18
-
6
-
21
18
+
=
135
1+3+5
=
9
=
9
=
9
-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
--
-
-
-
-
-
-
6
6
21
18
-
6
6
21
18
-
6
6
21
18
+
=
153
1+5+3
=
9
=
9
=
9
-
-
6
6
3
9
-
6
6
3
9
-
6
6
3
9
+
=
72
7+2
=
9
=
9
=
9
-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
ONE
1
-
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
2
-
-
-
-
-
-
-
-
-
3
-
-
-
-
3
-
-
-
-
3
-
-
-
3
occurs
x
3
=
9
=
9
4
--
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
FIVE
5
-
-
-
-
-
-
-
6
6
-
-
-
6
6
-
-
-
6
6
-
-
-
-
6
occurs
x
6
=
36
3+6
9
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
9
-
-
-
-
9
-
-
9
occurs
x
3
=
27
2+7
9
27
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
27
-
-
12
-
72
-
27
2+7
1+2
-
-
-
9
-
-
-
-
9
-
-
-
-
9
-
-
2+7
-
-
1+2
-
7+2
-
2+7
9
3
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
9
-
-
3
-
9
-
9
-
-
6
6
3
9
-
6
6
3
9
-
6
6
3
9
-
-
-
-
-
--
-
-
-
-
9
3
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
9
-
-
3
-
9
-
9

 

 

-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
--
-
-
-
-
-
-
-
6
-
-
-
-
6
-
-
-
-
6
-
-
+
=
18
1+8
=
9
=
9
=
9
-
-
-
15
-
-
-
-
15
-
-
-
-
15
-
-
+
=
54
5+4
=
9
=
9
=
9
-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
--
-
-
-
-
-
-
6
-
3
9
-
6
-
3
9
-
6
-
3
9
+
=
54
5+4
=
9
=
9
=
9
-
-`
6
-
21
18
-
6
-
21
18
-
6
-
21
18
+
=
135
1+3+5
=
9
=
9
=
9
-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
--
-
-
-
-
-
-
6
6
21
18
-
6
6
21
18
-
6
6
21
18
+
=
153
1+5+3
=
9
=
9
=
9
-
-
6
6
3
9
-
6
6
3
9
-
6
6
3
9
+
=
72
7+2
=
9
=
9
=
9
-
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
3
-
-
-
-
3
-
-
-
-
3
-
-
-
3
occurs
x
3
=
9
=
9
-
-
6
6
-
-
-
6
6
-
-
-
6
6
-
-
-
-
6
occurs
x
6
=
36
3+6
9
-
-
-
-
-
9
-
-
-
-
9
-
-
-
-
9
-
-
9
occurs
x
3
=
27
2+7
9
27
12
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
27
-
-
12
-
72
-
27
2+7
1+2
-
-
-
9
-
-
-
-
9
-
-
-
-
9
-
-
2+7
-
-
1+2
-
7+2
-
2+7
9
3
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
9
-
-
3
-
9
-
9
-
-
6
6
3
9
-
6
6
3
9
-
6
6
3
9
-
-
-
-
-
--
-
-
-
-
9
3
F
O
U
R
-
F
O
U
R
-
F
O
U
R
-
-
9
-
-
3
-
9
-
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
FOUR FOUR FOUR
-
-
-
-
-
-
-
-
-
-
-
-
-
F
=
6
1
1
F
6
6
6
-
1
2
-
4
5
6
7
8
-
O
=
3
2
1
O
15
6
6
-
1
2
-
4
5
6
7
8
-
U
=
3
3
1
U
21
3
3
-
1
2
3
4
5
-
7
8
-
R
=
9
4
1
R
18
9
9
-
1
2
-
4
5
-
7
8
9
F
=
6
5
1
F
6
6
6
-
1
2
-
4
5
6
7
8
-
O
=
3
6
1
O
15
6
6
-
1
2
-
4
5
6
7
8
-
U
=
7
7
1
U
21
3
3
-
1
2
3
4
5
-
7
8
-
R
=
9
8
1
R
18
9
9
-
1
2
-
4
5
-
7
8
9
F
=
6
9
1
F
6
6
6
-
1
2
-
4
5
6
7
8
-
O
=
3
10
1
O
15
6
6
-
1
2
-
4
5
6
7
8
-
U
=
7
11
1
U
21
3
3
-
1
2
3
4
5
-
7
8
-
R
=
9
12
1
R
18
9
9
-
1
2
-
4
5
-
7
8
9
-
-
72
-
12
FOUR FOUR FOUR
153
72
72
-
1
2
9
4
5
36
7
8
18
-
-
7+2
-
1+2
-
1+5+3
7+2
7+2
-
-
-
-
-
-
3+6
-
-
1+8
-
-
9
-
3
FOUR FOUR FOUR
9
9
9
-
1
2
9
4
5
9
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
FOUR FOUR FOUR
-
-
-
-
-
-
-
-
-
-
-
-
-
U
=
3
3
1
U
21
3
3
-
1
2
3
4
5
-
7
8
-
U
=
7
7
1
U
21
3
3
-
1
2
3
4
5
-
7
8
-
U
=
7
11
1
U
21
3
3
-
1
2
3
4
5
-
7
8
-
F
=
6
1
1
F
6
6
6
-
1
2
-
4
5
6
7
8
-
O
=
3
2
1
O
15
6
6
-
1
2
-
4
5
6
7
8
-
F
=
6
5
1
F
6
6
6
-
1
2
-
4
5
6
7
8
-
O
=
3
6
1
O
15
6
6
-
1
2
-
4
5
6
7
8
-
F
=
6
9
1
F
6
6
6
-
1
2
-
4
5
6
7
8
-
O
=
3
10
1
O
15
6
6
-
1
2
-
4
5
6
7
8
-
R
=
9
4
1
R
18
9
9
-
1
2
-
4
5
-
7
8
9
R
=
9
8
1
R
18
9
9
-
1
2
-
4
5
-
7
8
9
R
=
9
12
1
R
18
9
9
-
1
2
-
4
5
-
7
8
9
-
-
72
-
12
FOUR FOUR FOUR
153
72
72
-
1
2
9
4
5
36
7
8
18
-
-
7+2
-
1+2
-
1+5+3
7+2
7+2
-
-
-
-
-
-
3+6
-
-
1+8
-
-
9
-
3
FOUR FOUR FOUR
9
9
9
-
1
2
9
4
5
9
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
3
6
9
-
-
-
-
-
FOUR FOUR FOUR
-
-
-
-
-
-
-
U
=
3
3
1
U
21
3
3
-
3
-
-
U
=
7
7
1
U
21
3
3
-
3
-
-
U
=
7
11
1
U
21
3
3
-
3
-
-
F
=
6
1
1
F
6
6
6
-
-
6
-
O
=
3
2
1
O
15
6
6
-
-
6
-
F
=
6
5
1
F
6
6
6
-
-
6
-
O
=
3
6
1
O
15
6
6
-
-
6
-
F
=
6
9
1
F
6
6
6
-
-
6
-
O
=
3
10
1
O
15
6
6
-
-
6
-
R
=
9
4
1
R
18
9
9
-
-
-
9
R
=
9
8
1
R
18
9
9
-
-
-
9
R
=
9
12
1
R
18
9
9
-
-
-
9
-
-
72
-
12
FOUR FOUR FOUR
153
72
72
-
9
36
18
-
-
7+2
-
1+2
-
1+5+3
7+2
7+2
-
-
3+6
1+8
-
-
9
-
3
FOUR FOUR FOUR
9
9
9
-
9
9
9

 

 

 

ONE 1 ONE
EIGHT 8 EIGHT
THREE 3 THREE
SIX 6 SIX

 

18
-
8
EIGHTEEN
73
46
1
36
-
9
THIRTY SIX
152
62
8
54
-
17
Add to reduce
225
108
9
5+4
-
1+7
Reduce to deduce
2+2+5
1+0+8
-
9
-
8
Essence of number
9
9
9

 

 

 

 

 

 

3
THE
33
15
6
6
FAMILY
66
30
3
9
First Total
99
45
45
-
Add to Reduce
9+9
4+5
4+5
9
Second Total
18
9
9
-
Reduce to Deduce
1+8
-
-
9
Essence of Number
9
9
9

 

 

3
THE
-
-
-
6
FAMILY
-
-
-
-
T
20
2
2
-
H
8
8
8
-
E
5
5
5
-
THE
-
-
-
-
F
6
6
6
-
A
1
1
1
-
M
13
4
4
-
I
9
9
9
-
L
12
3
3
-
Y
25
7
7
-
FAMILY
-
-
-
9
Add to Reduce
99
45
45
-
Reduce to Deduce
9+9
4+5
4+5
9
Essence of Number
18
9
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
FAMILY
-
-
-
-
-
-
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
FAMILY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
9
-
99
45
45
-
1
2
3
4
5
6
7
8
9
-
-
4+5
-
-
-
9+9
4+5
4+5
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
-
18
9
9
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
FAMILY
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
FAMILY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
9
-
99
45
45
-
1
2
3
4
5
6
7
8
9
-
-
4+5
-
-
-
9+9
4+5
4+5
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
-
18
9
9
-
1
2
3
4
5
6
7
8
9

 

 

3
THE
-
-
-
6
FAMILY
-
-
-
-
A
1
1
1
-
T
20
2
2
-
L
12
3
3
-
M
13
4
4
-
E
5
5
5
-
F
6
6
6
-
Y
25
7
7
-
H
8
8
8
-
I
9
9
9
3
THE
-
-
-
-
FAMILY
-
-
-
9
Add to Reduce
99
45
45
-
Reduce to Deduce
9+9
4+5
4+5
9
Essence of Number
18
9
9

 

 

 

 

 
 
Top
  
 
Evokation
  
Previous Page
Index
 Next Page